Экономика и менеджмент \ Эконометрика

Оцінювання параметрів і перевірка статистичних гіпотез у випадку вибірок малого об’єму. Моделювання зростання прибутку фірми. Визначення оптимальної поліноміальної регресії, страница 26

t

1

2

3

4

5

6

7

8

9

Y

19,2

18,6

18,1

17,5

18,2

18,8

20

22,3

24,4

Необхідно:

1    Методом ортогональних многочленів побудувати поліноміальні регресії 1-го, 2-го,…, m-го порядків залежності середньої урожайності зернових від номеру року.

2  Для кожної регресії, починаючи з 3-го порядку, обчислити коефіцієнт детермінації і при рівні значущості =0,05, перевірити значимість нового коефіцієнту за допомогою:

а) критерію Стьюдента; б) критерію Фішера.

3  Визначити оптимальний ступінь поліноміальної регресії, вважаючи, що поліпшення результату не відбувається, якщо два останніх коефіцієнти виявилися незначущими. Оцінити якість оптимальної регресії.

4  Зробити прогноз урожайності зернових на поточний і наступний роки.

Розв’язання

Побудову оптимальної поліноміальної регресії будемо здійснювати за допомогою ортогональних многочленів.

Система многочленів  ‑ нульового ступеня,  ‑ першого ступеня, …,  ‑ m-ой ступеня називається ортогональної, якщо при

,

де t1, t2,..., tn – значення моментів часу t, у цьому випадку рівні
1, 2, …, n відповідно.

При цілочисельних значеннях аргументу (t=i, i N) систему ортогональних многочленів можна задати формулами:

 

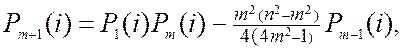   m = 1, 2,  ...   (3.1)

Наприклад,         

Для необхідних далі сум  зручно користуватися рекурентною формулою

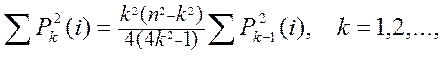              (3.2)

де

Використання ортогональних многочленів дозволяє побудувати поліноміальну регресію m-го порядку за допомогою рекурентною формули

,                          (3.3)

де  ‑ поліноміальна регресія (m-1)-го порядку,  ‑ поправка, яка уточнює модель (m-1)-го порядку.

Оцінка  коефіцієнта регресії  визначається формулою

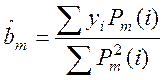.                                         (3.4)

Значимість оцінки  коефіцієнта регресії  визначається або за критерієм Стьюдента, або за критерієм Фішера, які рівносильні. Якщо оцінка  виявляється значимою, то це озна­чає, що коефіцієнт регресії  відмінний від нуля і поправка  є значимою. У противному випадку вважаємо, що =0, тобто поправка  не поліпшує модель (m-1)-го порядку.

Згідно критерію Стьюдента оцінка  вважається значимої, якщо виконується нерівність

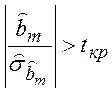,                                             (3.5)

де  ‑ критичне значення розподілу Стьюдента, що обчислюється при рівні значимості  і числі ступенів волі
n-m-1,  ‑ оцінка дисперсії випадкової величини , що визначається за формулою,

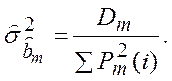                                            (3.6)

Відповідно до критерію Фішера оцінка  вважається значимої, якщо виконується нерівність

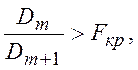                                 (3.7)

де  ‑ критичне значення розподілу Фішера, що обчислює при рівні значимості  і числах ступенів волі n-m-1 і n-m-2.

Будемо виходити з того, що дисперсія  моделі m-го порядку визначається формулою

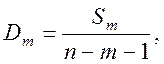                             (3.8)

де, n – об’єм вибірки, m<n-1,  ‑ залишкова сума квадратів моделі m-го порядку, для якої має місце рекурентне співвідношення

.                              (3.9)

Коефіцієнт детермінації  моделі m-го порядку у випадку ортогональних моделей обчислюється за формулою

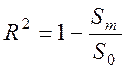                                      (3.10)

і визначає якість моделі.

Складаємо розрахункову табл. 3.2.

Таблиця 3.2

i

yi

P1(i)

yi1(i)

P2(i)

yi2(i)

P3(i)

yi3(i)

P4(i)

yi4(i)

1

19,2

-4

-76,8

9,33

179,20

-16,8

-322,56

24,00

460,80

2

18,6

-3

-55,8

2,33

43,40

8,4

156,24

-36,00

-669,60

3

18,1

-2

-36,2

-2,67

-48,27

15,6

282,36

-18,86

-341,31

4

17,5

-1

-17,5

-5,67

-99,17

10,8

189,00

15,43

270,00

5

18,2

0

0

-6,67

-121,33

0

0

30,86

561,60

6

18,8

1

18,8

-5,67

-106,53

-10,8

-203,04

15,42

290,06

7

20,0

2

40,0

-2,67

-53,33

-15,6

-312,00

-18,86

-377,14

8

22,3

3

66,9

2,33

52,03

-8,4

-187,32

-36,00

-802,80

9

24,4

4

97,6

9,33

227,73

16,8

409,92

24,00

585,60

Σ

177,1

0

37,0

0

73,73

0

12,60

0

-22,80
Скачать файл