Оцінка локальної похибки і організація обчислень, страница 3

                                                                                                 (10.56)

де

               

Тут R(J_n) — спектральний радіус матриці Якобі J_n зумовлений її найбільшим власним значенням λ_тах, яке знаходиться степеневим методом (див. розділ 4). Умова переходу від неявного метод до явного визначається співвідношенням

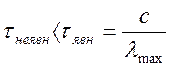                                                                           (10.57)

Умова зворотного переходу — від явного методу до неявного — набуває вигляду де γ — співвідношення обчислювальних витрат на виконання кроку неявним і явним методами

Застосування такого підходу дозволяє прискорити обчислення на 20-30 % у разі збереження похибки розв'язку [22]

10.10.   ЯвнінелінійніметодизА-стійкістю

Останнім часом ведуться інтенсивні дослідження з метою побудови явних ме­тодів розв'язання жорстких задач із підвищеною стійкістю, стійкість яких на­ближалася б до стійкості неявних методів. Оскільки, як було показано, для лі­нійних методів таких можливостей не існує, пошук ведеться серед нелінійних. Певні успіхи можна продемонструвати на прикладах явних нелінійних методів першого і другого порядків.

10.10.1. Явний нелінійний метод першого порядку

Відмовимося від експонентної апроксимації розв'язку диференціального рів­няння, обумовленого власними значеннями матриці Якобі від його правої час­тини (10.4), і перейдемо до часової апроксимації на інтервалі

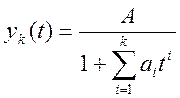                                                                                                 (10.59)

Тоді, колимаємо гіперболічну апроксимуючу функцію:

                

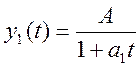
що відповідає нелінійній формулі наближення, запропонованій Федулою:

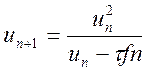                                                                                                        (10.60)

Покажемо, користуючись тестовим рівняннямщо, коли

формула (10.60) має А -  стійкість, яка збігається зі стійкістю неявного методу Ейлера. Дійсно, на підставі співвідношення (10.60) можна записати:

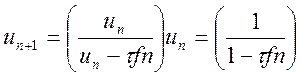                                                                                  (10.61)

Із виразу (10.61) випливає, що, колиза будь-якого довільного кроку т

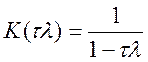                                                                  (10.62)

Приклад 10.6

Розв'яжемо явним нелінійним методом Федули рівняння              розв'язане раніше, в прикладі 10.1, неявним методом Ейлера. Потрібно, як і раніше, з кро­комзнайти значення y(0,4).

Користуючись формулою (10.60), запишемо програму розв'язання задачі засобами паке­та Mathematical

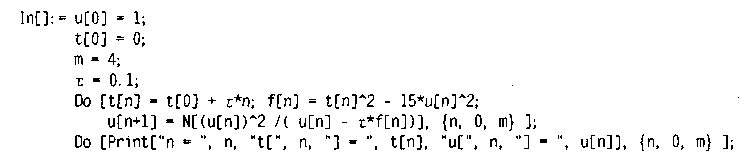
Отримані результати дещо відрізняються від результатів прикладу 10.1:

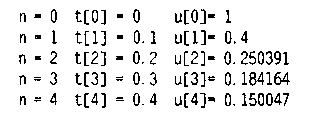
Цікаво порівняти результати розв'язання одного й того ж самого рівняння, отримані в прикладах 10.1, 10.2, 10.3 і 10.6 різними неявними методами (табл. 10.2). Тут же наве­дено розв'язання неявним методом BDF п'ятого порядку як найбільш точне.

Таблиця 10.2. Порівняльні результати обчислення

Метод                                                                                                                                    Значення y(0,4)

Явний метод Ейлера першого порядку                                                                                              -8,10207

Неявний метод Ейлера першого порядку                                                                                          0,212276

Неявний метод Ракитського другого порядку                                                                          0,155192

Неявний метод Гіра-Шихмана другого порядку

зі значенням y[0,1], отриманим неявним методом Ейлера    0.146298