Основні проблеми чисельного розв’язання задач. Класифікація похибок, страница 4

Це питання вирішується шляхом знаходження визначника й порівняння його з нулем. У випадку, коли елементи визначника задані точно, варто обчислити визначник і правильно відповісти на поставлене в задачі питання.

У випадку, коли елементи визначника задані наближено з відносною похибкою d, питання є складнішим. Нехай елементи матриці позначені через  . Тоді кожен елемент матриці  тепер уже не дорівнює конкретному значенню, а може набувати будь-якого значення з відрізка [(1-d); (1+d)], якщо > 0 , і з відрізка [(1+d); (1-d)], якщо < 0. Множина всіх можливих значень елементів матриці являє собою замкнену обмежену множину в 9-вимірному просторі. Сам визначник є неперервною й диференційованою функцією 9 змінних - елементів матриці . За відомою теоремою Вейєрштрасса ця функція досягає на зазначеній множині свого найбільшого та найменшого значень M і m. Якщо відрізок [ m, M ] не містить точку 0 , то це означає, що при будь-яких припустимих значеннях елементів матриці  визначник не набуває значення 0. Якщо ж точка 0 належить відрізку [m, M], таке твердження буде неправомірним. Буде мати місце невизначеність.

З’ясувати m і M допомагають наступні міркування. Як функція своїх аргументів (елементів матриці ) визначник має таку властивість (принцип максимуму): ця функція досягає свого найбільшого і найменшого значень завжди на границі області . Більше того, можна довести, що ці значення досягаються в точках, координати яких мають вигляд (1±d). Таких точок 2=512. У кожній з них варто обчислити визначник, а потім вибрати з отриманих значень найбільше та найменше. Це й будуть числа M і m.

1.3 Середні квадратичні похибки

Нехай передбачається проведення серії вимірів деякої величини X. У кожному з вимірів буде отримане якесь її значення, причому  залежно від точності приладу, зокрема, ці значення будуть знаходитися в деякому інтервалі, загальне їх число скінченне. Позначимо ці значення , їх ймовірності . Оскільки заздалегідь невідомо, яке значення величини Х буде отримано в кожному вимірі, ця величина є випадковою.

Математичне очікування Х виражається формулою

M[X]=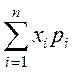 .                                (1.6)

Про якість вимірів, тобто ступінь розкиду помилок виміру, можна роб висновкиити за розмірами дисперсії, або середнього квадратичного відхилення випадкової величини:

D[X]=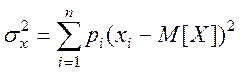.             (1.7)

Величина  називається в теорії похибок середньою квадратичною похибкою вимірювання.

Якщо результати вимірювання є незалежними, тобто результат довільного виміру не залежить від того, які результати отримані в інших вимірах, для них прийнятні теореми Чебишева і Бернуллі. Зокрема, бувають наступні припущення.

1 Якщо випадкова величина Х набyває тільки невід’ємних значень, частина яких менша деякого додатного числа а, то

p[(X<a)]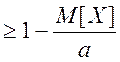.                            (1.8)

2 Якщо а > 0, то

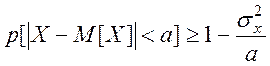.                  (1.9)

Відзначимо, що формулою (1.7) користуються для обчислення середніх квадратичних похибок і в детермінованих процесах

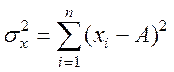
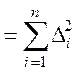,                 (1.10)

де А —точне значення числа X, а  — абсолютні похибки.

1.4  Поширення похибок

Важливим у чисельному аналізі є питання про те, як помилка, що виникла у визначеному місці в ході обчислень, поширюється далі, тобто чи стає її вплив більшим або меншим залежно від того, як виконуються наступні операції. Сформулюємо деякі правила оцінки похибок при виконанні операцій над наближеними числами:

- при додаванні або відніманні чисел їхні абсолютні похибки додаються;

- при множенні або діленні чисел їхні відносні похибки додаються.

Ці правила можна вивести безпосередньо. Нехай є два наближення a₁ і а₂ до чисел x₁ і x₂, а також відповідні абсолютні похибки ,

Оцінимо, наприклад, похибку суми

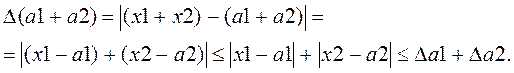
Для визначення оцінок похибки арифметичних дій можна використовувати загальне правило оцінки похибки функції.

Розглянемо функцію y=f(x). Нехай а – наближене значення аргумента х,  - його абсолютна похибка. Абсолютну похибку функції можна вважати її приростом, який можна замінити диференціалом . Тоді одержимо , .

Застосуємо загальне правило, наприклад, для оцінки похибки суми f(x₁,x₂)=x₁+x₂

та добутку f(x₁,x₂)=x₁x₂

Тут через а₁ і а₂ позначені значення величин х₁ і х₂, задані з абсолютними похибками а₁ і а₂.