Основні проблеми чисельного розв’язання задач. Класифікація похибок, страница 3

Припустимо, що величини а і b обчислені з похибками, що не перевищують 1% їх точних значень, а=140,62, b=37,62. Обчислюючи величину  за формулою (1.1) із наближеними значеннями,   одержимо         с=140,62-137,62=3,0. Отже, похибки в обчисленні вихідних величин а і b призвели до десятикратного збільшення числа .

1.2   Абсолютна і відносна похибки

Абсолютна похибка - це модуль різниці між відповідним точним значенням розглянутої величини А і наближеним її значенням а. Вона має вигляд

.                     (1.2)

Безпосередньо за значенням абсолютної похибки досить важко робити висновок про ступінь розбіжності між точним значенням  величини і його наближеним значенням. Так, похибка 2м цілком припустима при визначенні відстані між Києвом і Сумами та абсолютно неприпустима при вимірюванні розмірів кімнати. Тому застосовується ще одна характеристика наближених величин — їх відносна похибка.

Відносною похибкою  наближеного значення величини, точне значення якої дорівнює А, називається відношення його абсолютної похибки  до модуля точного значення, тобто

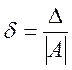    .                                (1.3)

Наприклад, нехай в результаті вимірювання довжини бігової доріжки отримано значення а=99,1м. Точне значення цієї величини = 100м. Абсолютна похибка  =0,9. Відносна похибка за формулою (1.3) становить .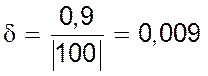

Із формул (1.2)—(1.3) бачимо, що абсолютна похибка має розмірність оцінюваних цією похибкою величин, відносна похибка завжди безрозмірна.

Величини  і  можуть бути обчислені точно лише в тих випадках, коли відоме не тільки наближене числове значення розглянутої величини, але і її точне значення. Останнє, однак, можливе далеко не у всіх випадках. Крім того, часто доводиться аналізувати похибки деякої множини наближених величин, наприклад, похибки вимірювання розмірів серії виготовлених деталей, викликані недосконалістю застосовуваних вимірювальних інструментів. Якість серії вимірювань для всіх деталей може оцінюватися найбільшою за модулем величиною абсолютної або відносної похибки їх розмірів. Тому часто вводяться поняття граничних абсолютної та відносної похибок.

За граничну абсолютну похибку * наближеного числа може бути взяте будь-яке число, не менше абсолютної похибки цього числа,

.                                       (1.4)

Аналогічно за граничну відносну похибку * наближеного числа може бути взяте будь-яке число, що задовольняє умову

.                                            (1.5)

При аналізі серії вимірювань за * і * беремо найбільші з отриманих відповідних значень  і  і тим самим визначаємо межі, всередині яких знаходяться відповідні похибки.

Значущими цифрами числа  називають усі цифри в його записі, починаючи з першої ненульової зліва. Значущу цифру числа  називають правильною, якщо абсолютна похибка числа не перевищує одиниці відповідного цій цифрі розряду.

Приклад 1 Для ряду 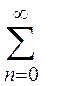 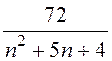знайти суму S аналітично. Обчислити значення часткових сум ряду S= 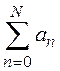і знайти величину похибки при значеннях =,,,,. Побудувати гістограму залежності правильних цифр результату від .

Знайдемо точну суму цього ряду:

S===,

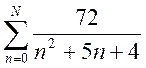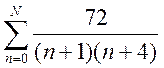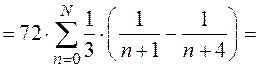
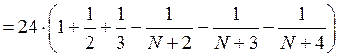Отже, .Уведемо функцію часткових сум S(N)=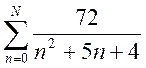.. Тоді абсолютну похибку можна визначити за допомогою функції d(N) = .

Результати обчислювального експерименту

N N	Значення частк. суми ряду S(N)	Абсолютна похибка d(N)	Кільк. правил. цифр Mi
110	S(10)=38.439560439	d(10) =5.56
1102	S(100)=43.3009269	d(100)=0.699	2
1103	S(1000)=43.9282153	d(1000)=0.072	3
1104	S(10000)=43.992802	d(10000)=0.0072	4
1105	S(100000)=43.99928021599	d(100000)=0.00072	5

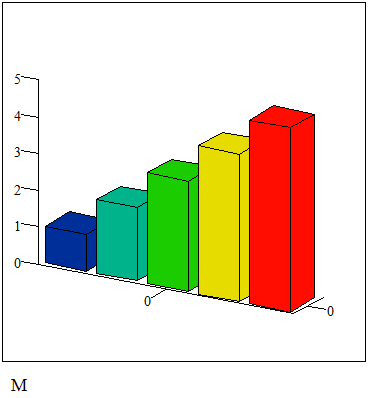
  Висновок. Як бачимо з наведеного обчислювального експерименту, збільшення числа членів ряду в 10 разів  порівняно з попереднім випадком збільшує число правильних цифр у відповіді на 1.

Гістограма

 

Приклад 2 Для матриці A=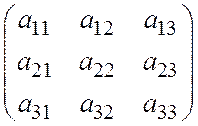 розв’язати питання про існування оберненої матриці  в таких випадках:

1)  елементи матриці задані точно;

 2) елементи матриці задані наближено з відносною похибкою  a)  та b) = b%.  Знайти відносну похибку результату.