










Міністерство освіти науки України
Сумський державний університет
Кафедра ІТП
Обов’язкове домашнє завдання
по дисципліні:
« Чисельні методи в інформатиці »
Виконав: студент групи ІТ-61
Руденко С.А.
Перевірив: Неня В.Г.
Суми 2008
120 Розділ 4. Обчислення власних значень і власних векторів матриці
4.3 Обчислення окремих власних значень
Якщо необхідно оцінити лише деякі з власних значень (наприклад, λmax або λmin ), то простіше використовувати степеневий метод для формування послідовності векторів
![]() , k=1,2,3….. (4.28)
, k=1,2,3….. (4.28)
Припустимо, що матриця А має n лінійно незалежних власних векторів xi і максимальне за величиною власне значення λmax=λt таке, що |λ1|>|λ2|>|λ3|>….>|λn|.
Якщо розкласти деякий ненульовий вектор z0 у базисі власних векторів матриці
![]() ,
,
то
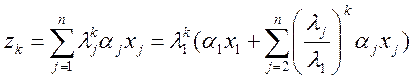 ,
k=0,1,2,…
,
k=0,1,2,…
Оскільки |λj/λ1| <1 для j> 2, то напрямок вектора zkпрямує до напрямку власного вектора хt якщо тільки а1≠ 0.
Для підвищення стійкості обчислень проводять масштабування послідовності векторів zk яке найпростіше здійснити, якщо перейти до послідовності уk нормуванням векторів zk за значеннями їх найбільших елементів zki, тобто замість виразу (4.28) використовують співвідношення:
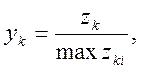
![]() , k=0,1,2,…., (4.29)
, k=0,1,2,…., (4.29)
при цьому
![]() (4.30)
(4.30)
і похибка визначення найбільшого власного значення прямує до нуля як (λj/λ1)k . Коли степеневий метод застосувати до оберненої матриці А-1, то аналогічно можна оцінити величину найменшого власного значення λmin , якщо виконується умова
![]()
Приклад 4.9
Знайдемо найбільше власне значення матриці з прикладу 4.5:
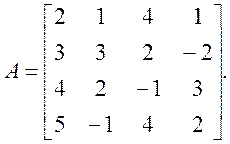
121 Розділ 4. Обчислення власних значень і власних векторів матриці
Спочатку, вибираючи вектор z0 = [1,1,1,1]Т, згідно з формулою (4.28) обчислюємо послідовність векторів zk+1за допомогою програми для пакета Mathcmatica:
In[]:=<<LinearAlgebra`MatrixManipulation`
A={{2, 1, 4, 1},
{3,3, 2, -2},
{4 , 2, -1, 3},
{5, -1, 4, 2}};
z[0]={1.,1.,1.,1.};
n=15
k[0]=First[Extract[z[0], Position[Abs[z[0]], VectorNorm[z[0]]]]];
Do [k[i]=First[Extract[z[i], Position[Abs[z[i]], VectorNorm[z[i]]]]];
z[i+1]=A .z[i]/k[i], {i, 0, n}]
Print[k[15]]
7.98298
Для кращого розуміння виконаної процедури відобразимо проміжні обчислення у більш наочній формі. На першій ітерації отримуємо:
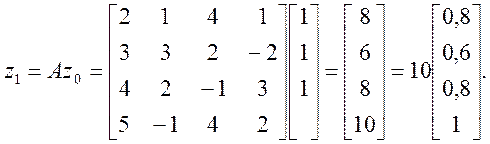
На другій інтерації згідно з виразом (4.29) обчислюємо
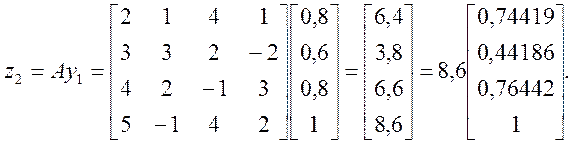
На третій інтерації отримуємо
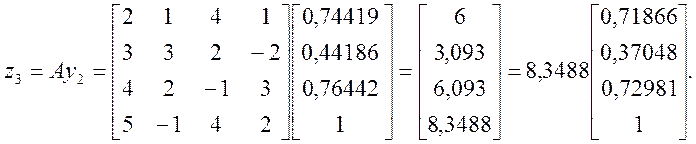
Нарешті, на п’ятнадцятій ітерації отримуємо:
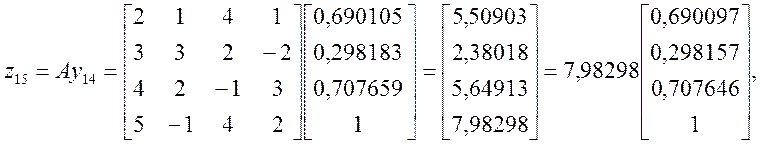
тобто шукане значення λmax=7,98298, яке добре збігається з результатом, отриманим у прикладі 4.5 за допомогою QR-алгоритму.
122 Розділ 4. Обчислення власних значень і власних векторів матриці
Приклад 4.10
Знайдемо найменше власне значення матриці з прикладу 4.5:
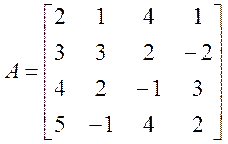
Для цього нам необхідна обернена матриця:
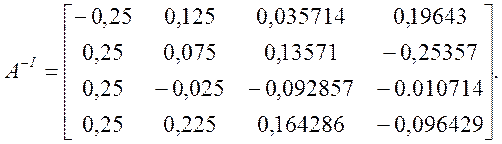
Виконаємо за аналогією з попереднім прикладом послідовність ітерацій, користуючись співвідношеннями (4.29) і обравши початковий вектор z0 =[1,1,1, 0]Т :
<<LinearAlgebra`MatrixManipulation`
A={{-0.25, 0.125, 0.0357143, 0.196429},
{0.25,0.075, 0.135714, -0.253571},
{0.25 , -0.025, -0.0928571, -0.0107143},
{0.25, -0.225, 0.164286, -0.0964286}};
z[0]={1.,1.,1.,0.};
n=15
k[0]=First[Extract[z[0], Position[Abs[z[0]], VectorNorm[z[0]]]]];
Do [k[i]=First[Extract[z[i], Position[Abs[z[i]], VectorNorm[z[i]]]]];
z[i+1]=A .z[i]/k[i], {i, 0, n}]
Print[k[15]]
15
-0.484893
Враховуючи, що ми отримали оцінку оберненої величини найменшого власного значення матриці, знаходимо:
1/k[15]
-2.06231
або 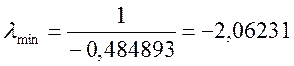 ,
,
що відповідає результату (λmin=-2,06237), який отримано в прикладі 4.5.
Степеневий метод можна поширити і на обчислення інших власних значень матриці, які за абсолютною величиною менші, ніж λmах або більші, ніж λmin. Для цього необхідно провести редукцію матриці, замінивши початкову матрицю іншою матрицею, яка не матиме вже знайдених значень λmах або λmin. Якщо матриці симетричні, така редукція здійснюється методом Хотелінга, який базується на використанні властивості ортогоиальності власних векторів матриці;
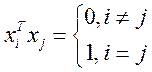 (4.31)
(4.31)
де компоненти векторів нормуються за значенням 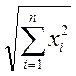 .
.
123 4.4. Власнізначеннястрічковихматриць
Нова матриця А2 будується на основі початкової матриці А1 яка має найбільше власне значення λ1= λmах так:
![]() (4.32)
(4.32)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.