Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 4

Як класи апроксимуючих функцій можуть виступати поліноміальні, тригонометричні, експонентні та ін.

На практиці досить важливим є випадок апроксимації функції многочленом

F(x) = a₀ + a₁x + a₂x² + …+ a_mx^m.

Якщо наближення будується на заданій дискретній множині точок {x_i}, то апроксимація називається точковою. До неї відносяться інтерполяція, середньоквадратичне наближення та ін. При побудові наближення на неперервній множині точок (наприклад, на відрізку [a,b]) апроксимація називається неперервною (або інтегральною).

Одним з основних типів точкової апроксимації є інтерполяція. У цьому випадку апроксимуюча функція проходить через задані вузлові точки. Іноді наближення табличних даних методом інтерполяції проводити незручно. Так, наприклад, якщо дані в таблиці неточні, то збіг значень інтерполяційної функції у вузлах з табличними даними означає, що вона точно повторює помилки таблиці. У таких випадках використовують інші види апроксимації, наприклад, метод найменших квадратів. Цим методом апроксимуюча функція будується так, щоб сума квадратів відстаней від ординат точок до лінії графіка апроксимуючої функції для однакових абсцис була найменшою.

5.1 Аналітичний опис результатів експериментів

За результатами n експериментів необхідно одержати залежність , що може показати,як у середньому y залежить від x. Таке рівняння називають рівнянням регресії.

Потрібно підібрати таку аналітичну залежність у= ,яка якнайкраще в умовах якогось заданого критерію описувала б отримані результати. При розв'язанні даної задачі найбільшого поширення набув метод найменших квадратів (МНК). Цим методом підбирається таке рівняння y= , при якому сума квадратів відхилень експериментальных значень від розрахункових , отриманих після підстановки x=x у це рівняння, набувала б мінімального значення. Аналітично ця вимога має вигляд

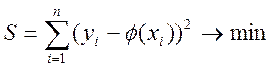
Піднесення до квадрату дозволяє позбутися впливу знака відхи-лення y від .

Природно,що застосування методу найменших квадратів вимагає задання вигляду рівняння y= .Його можна задати або виходячи з теоретичних передумов , або аналізуючи характер поля експериментальних точок. Тому рівняння регресії повинно бути записане як y= а сума

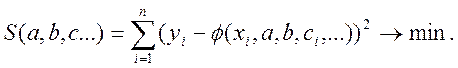    (5.1)

При заданому вигляді рівняння регресії необхідно підібрати такі значення невідомих коефіцієнтів а,b,c і ін.,що забезпечили б мінімум суми(5.1). Її можна вважати функцією від a,b,c та ін. Зви-чайно розглядаються лише такі y= які диферен-ційовані за всіма коефіцієнтами.За цієї умови знаходження набору значень коефіцієнтів ,що мінімізує S ,перетворюється у відому задачу математичного аналізу - пошук мінімуму функції декіль-кох змінних. Необхідною умовою екстремуму функції S(a,b,c) є справдження рівностей

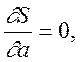
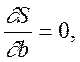
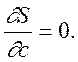                                    (5.2)

Використовуючи правила диференціювання, рівнянням (5.2) можна надати вигляд

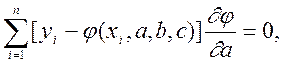
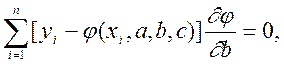                           (5.3)

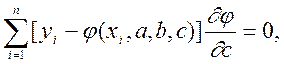
де 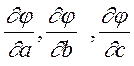-часткові похідні функції y=.

Достатня умова мінімуму функції декількох змінних поля-гає в позитивній визначеності матриці Гессе, складеної з похід-них другого порядку в критичній точці.

У випадку знаходження мінімуму методом найменших квадратів можна не перевіряти матрицю Гессе, тому що функція, яка обмежена знизу , необмежена зверху і має тільки одну підозрі-лу на екстремум точку, може набувати в ній тільки мінімум.                                                                                 

Вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вихідними даними обчислюють середні значення х_ср та у_ср :

,  ,  ,

    .

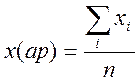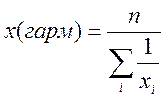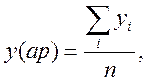
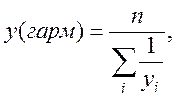
Величина обчислюється так:

1) якщо  збігається з одним із вихідних , то ;

2) якщо  знаходиться між  і ,  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і , за формулою

.

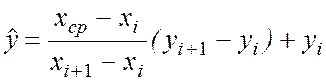Вибір рівняння регресії здійснюється шляхом пошуку міні-мального значення виразу 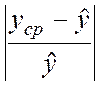 і відповідної йому функції.

5.3 Постановка задачі інтерполяціїю Інтерполяційний многочлен Лагранжа.