Метод простих ітерацій. Метод Ньютона. Розв’язування систем лінійних алгебраїчних рівнянь (СЛАР), страница 12

9.6.1 Явні різницеві схеми

Розглянемо мішану задачу для рівняння теплопровідності зі сталими коефіцієнтами. В області {0<x<1,0<tT} потрібно знайти розв'язок рівняння

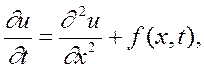                                                                                                       (9.22)

що задовольняє початкову умову

u(х,0)=u⁰(x), 0                                                                                                        (9.23)

і граничні умови

u(0,t)=(t), u(1,t)=(t).                                                                                                 (9.24)

Як відомо, при таких припущеннях щодо гладкості розв’язок задачі (9.22) — (9.24) існує і єдиний. При вивченні апроксимації різницевими схемами припустимо, що розв’язок u(x,t) має необхідну кількість похідних по t і x. Розв’язок задачі (9.22) —(9.24) неперервно залежить від початкових та граничних даних.

При побудові різницевої схеми введемо сітку в області змінних і задамо шаблон, тобто множину точок сітки, що бере участь в апроксимації диференціального виразу. Сітка вводиться за змінною x із кроком h=∆x так:

 , ,                                                  

а за змінною t із кроком t (позначимо її ,  )

Точки , j=0,1,…,N, m=0,1,…,K утворюють вузли просторово - часової сітки. Вузли, що належать відрізкам , ,  належать до граничних вузлів сітки , а всі інші вузли —внутрішні.

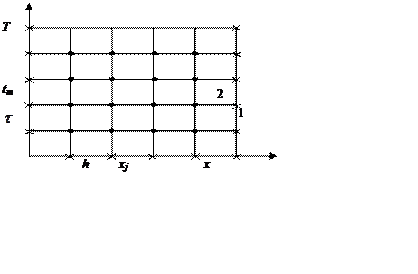
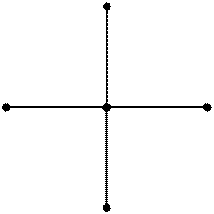
                                    Рис. – 9.2

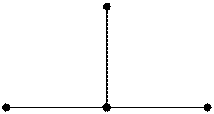
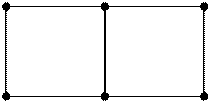
На рис. 9.2 позначено 1 — граничні, 2 — внутрішні вузли сітки. Варіанти шаблонів наведені на рис. 9.3.

Шаром називається множина всіх вузлів сітки, що мають одну й ту саму часову координату. Таким чином, n-м шаром буде множина вузлів ,,…,. Для функцій  та , визначених на сітці , введемо позначення: . А для частинних похідних оберемо такі наближення:

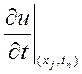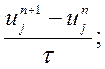=                             (9.25)

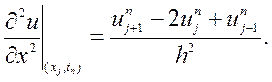                                                                                                                                          (9.26)

Для апроксимації рівняння (9.22) у точці  введемо шаблон (рис.9.3,а). Отримаємо різницеву схему

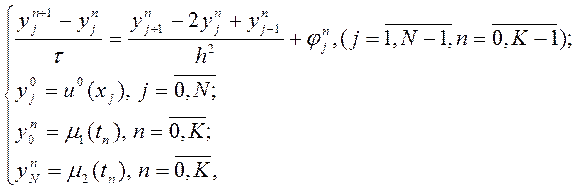  (9.27)

де  - це значення сіткової функції, що наближає точне значення розв’язку у вузлі .

                                    

         (                          

        Рис. – 9.3 а)                                     Рис. – 9.3 б)

                            

                         

                                                                    

     Рис. – 9.3 в)                                             Рис. – 9.3 г)

Дослідження різницевих схем передбачає відповідь на такі питання:

1)  існування та єдиність розв'язку;

2)  методи отримання розв'язку різницевої схеми;

3)  як співвідносяться різницева схема та вихідна диференціальна задача (проблема апроксимації);

4)  чи збігається наближений розв'язок до точного.

Розглянемо перше з рівнянь (9.27) відносно .

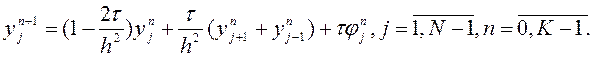  (9.28)

При  отримаємо

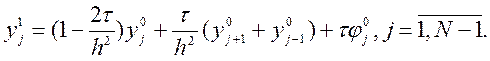
У правій частині всі значення відомі з крайових умов. Тому можна отримати шукану сіткову функцію на всьому першому часовому шарі. Аналогічно можна розрахувати другий і наступні шари. Звідси зрозуміло, що розв'язок існує і він єдиний. Оскільки всі формули  явні, то і вся схема є явною різницевою схемою.

Похибка різницевої схеми (9.27) визначається як різниця між розв’язками вихідної задачі (9.22) – (9.24) та задачі (9.27). Якщо підставити точний розв’язок у різницеве рівняння (9.27), то воно задовольниться не повністю, а з деякою похибкою, яка називається локальною похибкою дискретизації, або нев’язкою. Визначимо її поведінку:

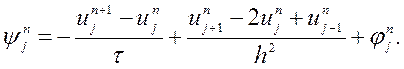
Для цього розкладемо та  в ряд Тейлора  через

.

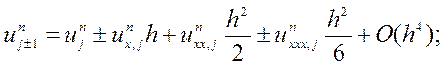
Тоді отримаємо вираз для нев’язки .

Вираз у дужках дорівнює нулю, оскільки  - точний розв’язок рівняння теплопровідності. Якщо взяти функції  так, що , то для нев’язки буде справедливою оцінка

.

Тобто наша різницева схема апроксимує диференціальне рівняння з другим порядком апроксимації по  і з першим порядком апроксимації по.