Верифікація програм. Семантики мов програмування, страница 3

Індуктивним твердженням для початкової точки повинна бути передумова P, а для завершальних – постумова Q. Таким чином, нарешті буде доведено, що Q– інваріант у кожній завершальній точці. З того, що Q - інваріант у кожній завершальній точці для передумови P, випливає часткова коректність програми.

Для даної блок-схеми запропонуємо  такі індуктивні твердження:

I_A :   P_sqrt ,

I_B :   z² ≤ x;  y₁ = (z+1)²; y₂ = 2z + 1,

I_C :   Q_{sqrt .}

 Крок 3 – доведення умов локальної коректності. На цьому кроці будуються умови локальної коректності і доводиться їх істинність.

Введемо додаткові позначення. Нехай α – деякий базовий шлях з контрольної точки S у контрольну точку T. Через R_α  позначимо формулу, яка істинна при переході через S тоді і тільки тоді, коли обчислення йде з цієї точки далі по шляху α. Ця формула називається умовою вибору шляху α.

Через θ_α  позначимо підстановку. Для змінної v  вираз θ_α(v)  має  значення  vпісля проходження  α, виражене через значення змінних перед проходженням α. Підстановка θ_α  називається перетворенням змінних, що відповідає шляху α. Вираз θ_α(I_K) буде означати результат застосування до формули I_K  підстановки θ_α , яка відповідає операторам присвоювання  шляху α.

Для нашої програми:

R_α :        true,

θ_α :       y₁ : = 1,      y₂ : = 1,      z : = 0,

R_β :       y₁ ≤ x ,

θ _β  :     y₂ : = y₁ + y₂ + 2,   y₂ : = y₂ + 2,   z : = z + 1,

R_γ :       y₁ > x ,

θ _β :       – ідентична підстановка.

У теорії Флойда доводиться таке твердження.

Припустимо, що індуктивне твердження для початкової точки є передумова P, і для будь-якого базового шляху α з контрольної  точки  S  у  контрольну  точку  Tформула   {I_S ,R _α }→ θ_α(I_T)  істинна при довільних значеннях змінних. Тоді для будь-якої точки S індуктивне  твердження   I_S   –  інваріант в  Sдля передумови P.

Якщо для шляху α вказана формула істинна, то шлях називається локально коректним. Сама формула називається умовою локальної коректності α.

Для нашої програми умови локальної коректності мають вигляд.

Шлях  α:

P_sqrt  →  θ_α (I_B) ,

або       (x ≥ 0)   →   { 0 ² ≤ x,   1 = (0+1)²,    1 = 2• 0 + 1} .

Шлях  β:

{ I_B ,   y₁ ≤ x }   →  θ_β (I_B) ,

або      { z ² ≤ x,  y₁ = (z+1)², y₂ = 2z + 1,  y₁ ≤ x }   →

→{(z+1)² ≤ x,  y₁+ y₂+2 =(z+2)²,  y₂ +2 =2(z+1)+1} .

Шлях  γ:

{ I_B ,   y₁ > x }   →  Q_sqrt ,

або       { z ² ≤ x,   y₁ = (z+1)², y₂ = 2z + 1, y₁ > x }   →

→{ z² ≤ x < (z+1)² } .

Можна далі показати, що програма завершується для будь-якого невід’ємного x. Це гарантує повну коректність програми.

Значний вклад у верифікацію програм було внесено Хоаром. Розглянемо коротко теорію Хоара.

Якщо для кожного оператора за заданими постумовами можна обчислити найслабшу передумову, то для програми можна побудувати коректне доведення. Результат, який треба одержати після виконання програми, береться як постумова останнього оператора. Далі програма відстежується від кінця до початку з послідовним обчисленням найслабших передумов для кожного оператора.

При  досягненні початку програми перша її передумова буде умовою, при якій програма видає необхідний результат.

Для простих операторів обчислення найслабшої передумови може бути задано аксіомою,  для більш складних операторів використовуються правила логічного виведення.

Аксіомою називаються логічний вираз, що передбачається правильним.

Правилом логічного виведення називається метод виведення істинності одного твердження на основі значень інших.

Семантику операторів будемо описувати вираженням  {P} S {Q}.

Оператор присвоювання

Нехай х := Е  – оператор присвоювання, а Q – його постумова.

Тоді передумова Р визначається аксіомою Р=Q_x=E , це означає, що передумова  Р обчислюється як умова Q , у якій всі  x  заміняють виразом Е.

Наприклад, для оператора x:= x-3 і постумови   {x>0}  найслабшою передумовою буде P: {x>3}.

Запис у формі {P} S {Q} має вигляд

                  {x>3}  x:=x-3       {x>0}.

Візьмемо            Р' = {x>5}, для  Р' справедлива рівність  Р' → Р.

Справедливий також запис

                        P'            S              Q

                        {x>5}   x:=x-3      {x>0} ,

хоча це і не випливає з нашої аксіоми. Для доведення потрібно ще використати правило логічного висновку.

Правила логічного висновку

Загальна форма правила логічного виведення має вигляд

                                    .

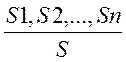Це означає, що з істинності S1,…,Sn випливає істинність S.

Правилами логічного виведення є, зокрема, правила логічного висновку:

1)         ,

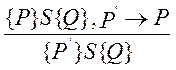       2)         .

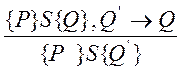Іншими словами, правило логічного висновку стверджує, що передумова завжди може бути посилена, а постумова ослаблена.