Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 9

Щоб помилка інтерполяції не перевищувала за абсолютною величиною деяке а, необхідно вибрати h, яке задовольняло б умову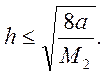

5.3 Метод найменших квадратів

Аналізуючи попереднє, можна зазначити, що інтерполювання може бути здійснене лише на невеликому інтервалі по кількох вузлах інтерполяції, процес обчислення скінченних різниць є нестійким. Окрім того, якщо значення  подають значення функції, яка наближується, зі значними похибками, інтерполювати ці значення недоцільно.

  За таких умов застосовують середньоквадратичне наближення. Найбільш ефективним методом побудови середньоквадратичного наближення функції є метод найменших квадратів (МНК).

  Нехай є відомими  значень  () деякої фізичної величини , виміряної у моменти часу . Припустимо, що ці значення подають істинні значення функції  у відповідні моменти часу зі значними похибками, значення яких невідомі, але припускається, що ці похибки є випадковими з математичним сподіванням, що дорівнює нулю. Будемо наближати невідому функцію  за допомогою лінійної комбінації деяких відомих  функцій

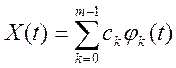,                   (5.39)

де функції ,, . . ., називатимемо базовими функціями. Потрібно визначити  невідомих коефіцієнтів  () з умови, щоб квадрат середньоквадратичного відхилення (СКВ) апроксимуючої функції  від апроксимованої (обчисленого для заданих значень  аргумента )

    (5.40)

був мінімальним (саме тому відповідний метод називається МНК). Квадрат СКВ (5.40) є функцією  невідомих коефіцієнтів  (). Тому для пошуку його мінімуму необхідно знайти  частинних похідних за окремими коефіцієнтами

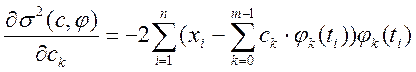        (5.41)

і прирівняти їх до нуля. В результаті одержується система з  лінійних алгебричних рівнянь з  невідомими ,,...,:

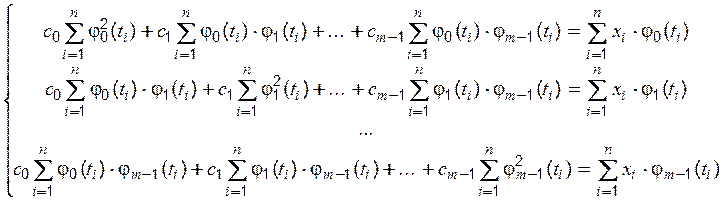(5.42)

Система (5.42) називається нормальною системою для методу найменших квадратів. Визначником цієї системи є визначник Грама сукупності функцій :

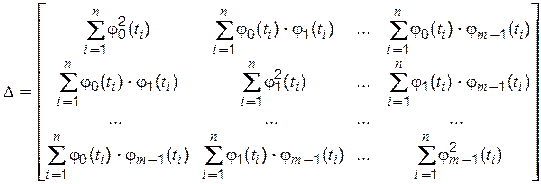 (5.43)

Як відомо, якщо функції   складають сукупність взаємонезалежних функцій (тобто ніяку з цих функцій неможливо подати як лінійну комбінацію решти з них), то визначник Грама цих функцій не дорівнює нулю. Це означає, що за базові функції при апроксимуванні потрібно обирати сукупності лінійно незалежних функцій. Тоді СЛАР (5.42) має єдиний розв'язок - значення коефіцієнтів  , що забезпечують мінімум квадрата середньоквадратичного відхилення апроксимуючої та апроксимованої функцій.

Ортогональними на деякому інтервалі  функціями називається сукупність таких функцій, що

.

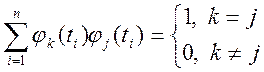Матриця Грама для ортогональних функцій є одиничною.

У випадку, коли за базові при апроксимуванні обрані ортогональні функції, обчислення коефіцієнтів апроксимації значно спрощується. У цьому випадку значення їх можна визначити співвідношенням

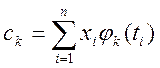.                     (5.44)

Тому при апроксимуванні бажано обирати за базові системи ортогональних функцій.

Класичними прикладами ортогональних функцій-поліномів є поліноми Якобі, Лежандра, Лагерра, Чебишева, Ерміта. Наприклад, поліноми Лежандра  є ортогональними на відрізку  і мають вигляд:

  ;;            ;;

;.

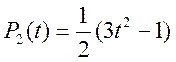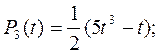
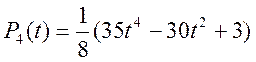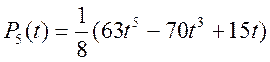  Поліноми Чебишева першого роду  є ортогональними також на інтервалі . Їх можна задати співвідношенням

;        ,

а рекурентна формула їх визначення має такий вигляд:

        ;           .

Наведемо приклади поліномів Чебишева першого роду:

;;;

;     ;

;   .

Поліноми Чебишева другого роду  також ортогональні на тому самому інтервалі і мають такий вигляд:

;;;

;            .

Поліноми Ерміта  ортогональні на всій числовій осі  і мають вигляд

;;;

;.

Наведені системи ортогональних поліномів стають у нагоді, коли за апроксимуючу функцію обирається поліном певного степеня, тобто для здійснення так званої поліноміальної апроксимації.

Прикладом системи неортогональних базових поліномів може бути така система:

;          ;...,;....

Вона часто використовується на практиці. Тоді - многочлен степеня . В цьому разі до розв’язку пропонується система  вигляду