26 t:=(xi-X[1])/h
27 return X[1]+(t/factorial(1))*DY[1]+((t*(t-1))/factorial(2))*D2Y[1]+((t*(t-1)*(t-2))/factotrial(3))*D3Y[1]+((t*(t-1)*(t-2)*(t-3))/factorial(4))*D4Y[1];
end
//R – дані сплайна
//eps – точність обчислень
//xi – значення аргумента, при якому потрібно знайти значення функції //
//відшукуємо значення кубічного сплайна в точці xi
Find_Spline(R,eps,xi)
1 linequ(R,R.length,1E-6,М)
2 k:=2
3 s31:=(X[k+1]-xi)*(X[k+1]-xi)*(2*(xi-X[k])+1)*Y[k]+(xi-X[k])*(xi-X[k])*(2*(X[k+1]-xi)+1)*Y[k+1]
4 s32:=(X[k+1]-xi)*(X[k+1]-xi)*(xi-X[k])*M[k]+(xi-X[k])*(xi-X[k])*(xi-X[k+1])*М[k+1]
5 return s31+s32
end
Оцінка похибки та збіжності при інтерполяції кубічними сплайнами
Якщо
![]() , то похибка інтерполяції кубічним сплайном
, то похибка інтерполяції кубічним сплайном
![]() , де
, де 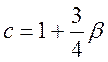 ,
, 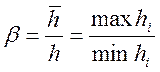 .
.
Якщо
![]() , r=1,2,3,4, то оцінка має вигляд
для
, r=1,2,3,4, то оцінка має вигляд
для ![]() .
.
Із
цих оцінок треба встановити збіжність інтерполяційного процесу на послідовності
сіток ![]() .
.
Для простоти обчислень або при труднощах у пошуку першої та другої похідних заданої функції можна застосувати таку оцінку похибок:
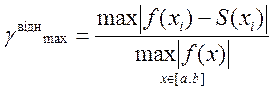 .
.
Приклад. Апроксимувати функції ![]() на відрізку [-2;2] , використовуючи
лінійний сплайн і природний кубічний сплайн.
на відрізку [-2;2] , використовуючи
лінійний сплайн і природний кубічний сплайн.
Дослідження проведемо на рівномірних сітках з кількістю вузлів інтерполяції : 5, 7, 9, 15 , 51 , 101 відповідно. Визначимо відносну похибку інтерполяції сплайнами на різних сітках. Результати занесемо до таблиці.
Аналіз результатів показує, що точність апроксимації істотно залежить від кількості вузлових точок.
|
Число вузлів |
Лінійний сплайн |
Кубічний сплайн |
Куб. сплайн по другій похідній |
|
5 |
0,0625 |
0,024 |
0,0092 |
|
7 |
0,0278 |
0,011 |
0,0038 |
|
9 |
0,0156 |
0,0061 |
0,002 |
|
15 |
0,0051 |
0,002 |
0,0007 |
|
51 |
0,0004 |
0,00016 |
0,000055 |
|
101 |
0,0001 |
0,000036 |
0,000014 |
Апроксимаційні властивості кубічного сплайна
Апроксимаційні
властивості кубічного сплайна залежать від гладкості функції ![]()
![]() - чим вище гладкість
інтерпольованої функції, тим вище порядок апроксимації при подрібленні сітки і
тим швидшою є збіжність.
- чим вище гладкість
інтерпольованої функції, тим вище порядок апроксимації при подрібленні сітки і
тим швидшою є збіжність.
Якщо
інтерпольована функція ![]() неперервна на відрізку
неперервна на відрізку ![]() , тобто
, тобто ![]() , то
, то
![]() при
при ![]() .
.
Якщо
інтерпольована функція ![]() має на відрізку
має на відрізку ![]() неперервну першу похідну, тобто
неперервну першу похідну, тобто ![]() , а
, а ![]() -
інтерполяційний сплайн, що задовольняє граничні умови 1-го або 3-го типу, то
при
-
інтерполяційний сплайн, що задовольняє граничні умови 1-го або 3-го типу, то
при ![]()
![]()
![]()
У цьому випадку не тільки сплайн збігається до інтерпольованої функції, але і похідна сплайна збігається до похідної цієї функції.
На
випадок, якщо ![]() , сплайн
, сплайн ![]() апроксимує
на відрізку
апроксимує
на відрізку ![]() функцію
функцію ![]() , а його
1-а та 2-а похідні апроксимують відповідно функції
, а його
1-а та 2-а похідні апроксимують відповідно функції ![]() та
та ![]() :
: ![]()
![]()
![]()
5.2.7 Застосування інтерполяції для складання таблиць
Теорія інтерполяції має застосування при складанні таблиць функцій. Одержавши завдання на складання таблиць тих чи інших функцій, математик повинен вирішити перед початком обчислень ряд питань. Повинна бути обрана формула, за якою будуть проводитися обчислення. Ця формула може змінюватися від ділянки до ділянки. Як правило, формули для обчислення значень функції бувають громіздкими і тому їх використовують для одержання деяких опорних значень і потім, шляхом субтабулювання, згущують таблицю. Формула, що дає опорні значення функції, повинна забезпечувати потрібну точність таблиць із врахуванням наступного субтабулювання . Якщо передбачається скласти таблиці з постійним кроком, то спочатку необхідно визначити крок таблиці.
Найчастіше таблиці функцій складаються так, щоб була можлива лінійна
інтерполяція ( тобто інтерполяція з використанням перших двох членів формули
Тейлора). У цьому випадку залишковий член буде мати вигляд 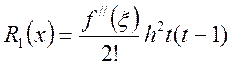 . Тут x належить інтервалу
між двома сусідніми табличними значеннями аргумента, у якому лежить х, а
. Тут x належить інтервалу
між двома сусідніми табличними значеннями аргумента, у якому лежить х, а ![]() . Добуток t(t – 1)
набуває найбільшого за модулем значення при
. Добуток t(t – 1)
набуває найбільшого за модулем значення при ![]() . Це
значення дорівнює
. Це
значення дорівнює ![]() Отже,
Отже, 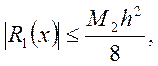 де
де ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.