Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 5

При цьому похибка наближення дорівнює R4=|f(0.14)-P₃(0.14)|<0.0001*0.4*0.6*1.6*2.6/4!= 4.16*10-6, або у MS Excel =ABS(F3*Q*(Q-1)*(Q-2)*(Q-3))/ФАКТР(4).

5.2.6 Інтерполяція за допомогою  сплайнів

  Підвищення точності інтерполювання вимагає збільшення вузлів інтерполяції. Це призведе до зростання степеня інтерполяційних многочленів. Але в умовах відсутності додаткової інформації про задану таблично функцію останні дають досить значну похибку. На практиці рідко проводять інтерполяцію поліномами степенів вище третього, тому що, по-перше, вони дають значні похибки й, по-друге, при нескінченному збільшенні порядку n інтерполяційного полінома Р_n(х) послідовність P_n не є збіжною (відповідно до теореми Фабера). Цей факт уперше виявив Рунге в 1901 р. В цьому випадку більш ефективним є використання сплайнів, що на проміжку між вузлами інтерполювання є поліномами невисокого степеня. На всьому проміжку інтерполяції  сплайн - це функція, що склеєна з різних частин поліномів. Отже, розглянемо на відрізку  систему вузлів . Сплайном  називається функція, що визначена на , має на ньому неперервні похідні  порядку і на кожному частковому відрізку  збігається з деяким многочленом степеня не вище . При цьому хоча б на одному з відрізків степінь многочлена дорівнює . Якщо , маємо інтерполюючий сплайн. Визначити сплайн можна також так.  Поліноміальним сплайном порядку m та дефекту k називається функція S_m,k(x) на сітці a=x₀<x₁<…<x_n-1<x_n=b така, що:

1) кожному проміжку ;

2)  число k називається дефектом сплайна, якщо , 0<k<m;

3)  розглянемо сплайн дефекту 1. S_m,1 = S_m. Інтерполяційним сплайном називається S_m(x), якщо S_m(x_i)=y_i,  i = 0, 1, …, n.

Лінійний інтерполяційний сплайн

Нехай  - розбиття відрізка : , - задані значення.

Сплайном першого степеня називається :неперервна на відрізку , лінійна на кожному частковому проміжку  функція f(x). Його позначення S₁(x) . Нехай . Вираз для сплайна S₁(x)  на цьому проміжку

           (5.26)

        y

                                                                            *

                                                                         *

                                                                              *

                                                 *

                                *

                                    *

                  *

       O                                                

 

                                          Рис. – 5.1

Залишковий член такої інтерполяції .

Оцінка залишкового члена залежить від диференціальних властивостей функції  f(x).

Нехай . Позначимо 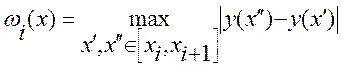- коливання функції f(x) на  проміжку  . Тоді використовується лема.

Лема (варіант теореми про середнє).

Нехай. Якщо величини  однакового знака, то існує точка  така, що .

За допомогою цієї леми доводиться теорема про оцінку залишкового члена лінійного інтерполяційного сплайна.

Теорема. Якщо , то .            Дійсно, , де 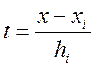. З наведеної вище леми маємо , де . Отже,

.

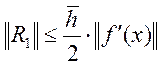З поліпшенням гладкості функції f(x) оцінка похибки її інтерполяції лінійними сплайнами також поліпшується. А саме, якщо , то , де .

  Для  можна одержати оцінку .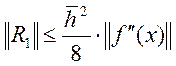

  Подальше збільшення гладкості функції f(x)  не дає підвищення порядку апроксимації. Відбувається насичення алгоритму.

Збіжність

Нехай на  задана послідовність сіток :,k=1,2,3…, які задовольняють умову  при . Для  будується інтерполяційний сплайн . Інтерполяційний процес вважається збіжним, якщо  при для будь-якої функції f(x) з деякого класу . Звідси випливає можливість інтерполяції з наперед заданою точністю

.

Перевага лінійних сплайнів у порівнянні з інтерполяційними многочленами полягає в тому, що з оцінки похибки випливає збіжність.