Математика \ Численные методы

Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 11

Приклад. Функція y=f(x) задана таблицею значень   у точках . Використовуючи метод найменших квадратів (МНК), знайти многочлен  найкращого середньоквадратичного наближення оптимального степеня m=m*. За оптимальне значення m* прийняти той степінь многочлена, починаючи з якого 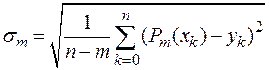стабілізується або починає зростати.

         Порядок   розв’зання  задачі:

1  Задати вектори x та  y вихідних даних.

2  Використовуючи функцію mnk , знайти многочлени Pm, m=0,1,2,..., за  методом  найменших квадратів. Обчислити відповідні їм значення .

3  Побудувати   гістограму залежності  від m, на підставі якої вибрати оптимальний степінь m* многочлена найкращого  середньоквадратичного  наближення.

4  На одному кресленні побудувати графіки многочленів Pm, m=0,1,2,..., m* і точковий графік вихідної функції.

  Вектори вихідних даних:

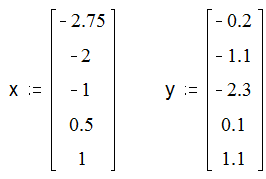 Функція mnk, що будує многочлен степеня m за  методом  найменших квадратів, повертає вектор a коефіцієнтів многочлена:

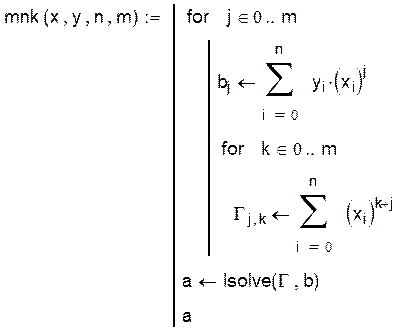
 - формуються вектор правих частин та матриця нормальної системи Гa=b методу найменших квадратів (базисні функції - 1, x, ,х2...,хm);

- lsolve(Г,b) – вбудована функція MATHCAD, що розв’язує систему лінійних алгебраїчних рівнянь .

Вхідні параметри:

 x, y - вектори вихідних даних;  n+1 - розмірність x,y.

Обчислення коефіцієнтів многочленів степеня 0,1,2,3 за методом найменших квадратів:

      

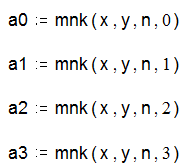
Функція P повертає значення многочлена степеня m у точці t; многочлен задається за допомогою вектора коефіцієнтів a: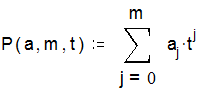

Функція  повертає значення середньоквадратичного відхилення многочлена P(a,m,t):
 


Обчислення значень ,m=0,1,2,3:

Гістограма

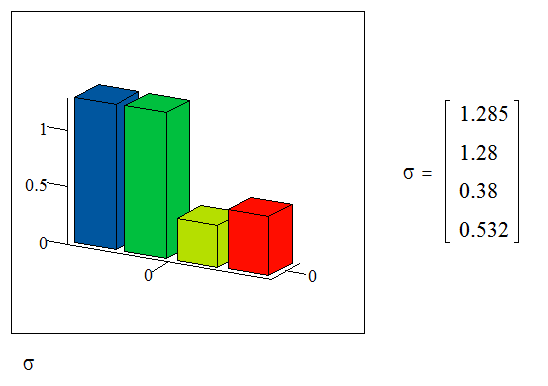
Висновок: оптимальний степінь m*=2; многочлен найкращого середньоквадратичного наближення: P2(x)=-1.102+1.598x+0.717

Графіки многочленів степеня 0,1,2 і точковий графік вихідної функції:

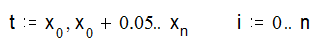
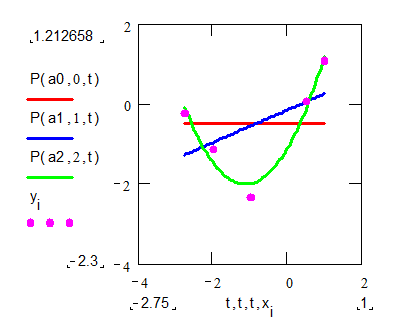
Приклад реалізації методу найменших квадратів на псевдокоді.

Нехай за допомогою зазначеного вище методу ми знайшли вигляд рівняння регресії

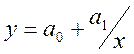, отже .

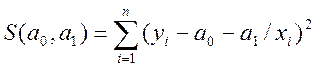Значення невідомих коефіцієнтів

.

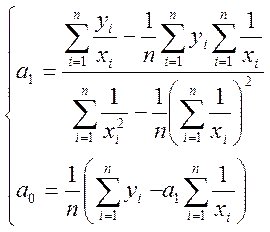Очевидно, що процедура, яка знайде розв’язки, буде простішою, якщо ми домовимося, що функції, що обчислюють відповідні суми, нами вже реалізовані:

//обчислення коефіцієнтів регресійної формули.

//X,Y – задані в умові масиви; a1,a0 – шукані коефіцієнти

//n – кількість заданих пар x,y в умові

Metod_Kvadr(n,X,Y,a1,a0):

1  a1:=(yixi(X,Y,n)-1/N)*yi(Y,n)*yi_na_1(X,n))/(yi_na_1_kw(X,n)-(1/n)*pow(yi_na_1(X,n),2));

2  a0:=(1./n)*(yi(Y,n)-a1*yi_na_1(X,n));

end

Питання і завдання до розділу 5

1  Постановка задач наближення функцій.

2  Метод найменших квадратів. Виведення нормальної системи методу найменших квадратів.

3  Обумовленість нормальної системи.

4  Вибір оптимального степеня апроксимуючого многочлена.

5  Поліноміальна інтерполяція. Многочлен у формі Лагранжа.

6  Многочлен у формі Ньютона.

7  Похибка інтерполяції.

8  Глобальна інтерполяція. Кусочно-поліноміальна інтерполяція. Вибір вузлів інтерполяції.

9  Інтерполяція із кратними вузлами.

10  Мінімізація оцінки похибки інтерполяції.

11  Інтерполяція сплайнами. Визначення сплайна. Лінійний сплайн.

12  Побудова кубічного сплайна.

13  Види граничних умов  при побудові сплайнів.

14  обудова параболічного сплайна.

15  нтерполяція функції  двох змінних.

16  Вивести нормальну систему методу найменших квадратів для визначення коефіцієнтів  функції:
 a) ; b) .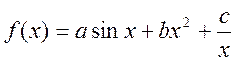

17  Використовуючи метод найменших квадратів, апроксимувати на відрізку  функцію многочленом першого степеня. Обчислити величину середньоквадратичного відхилення.

18  Побудувати інтерполяційний многочлен у формі Лагранжа й у формі Ньютона для функції , заданої таблицею значень.

Скачать файл