Апроксимація функцій. Поняття про наближення функцій. Iнтерполювання функції, страница 10

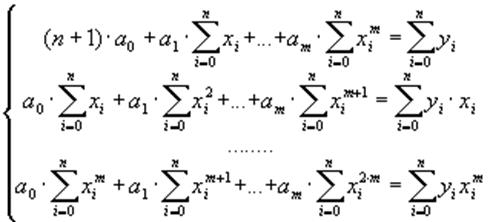
При  отриманий многочлен збігається з інтерполяційним многочленом Лагранжа.

Приклад. Найпростіша емпірична формула .

Про придатність цієї формули можна робити висновки за величинами 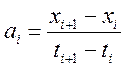. Якщо , то формула підходить. Невідомі коефіцієнти  знайдемо з необхідної умови екстремуму функції

.

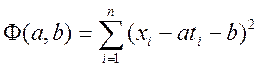У результаті одержимо систему лінійних рівнянь

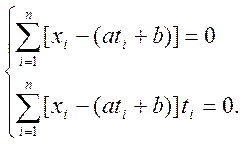
Розв’язуючи систему ,знаходимо a і b , що при заданому вигляді рівняння регресії забезпечують мінімум (a,b) .

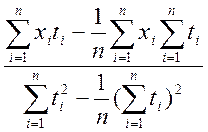a= ;     b=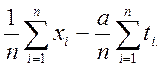

При цьому, природно, у результаті апроксимування певної сукупності даних в усіх випадках одержується однаковий поліном. Різниця полягає лише у зручності, простоті отримання коефіцієнтів цього полінома.

Якщо при поліноміальній апроксимації кількість базових функцій-поліномів дорівнює 2, тобто , апроксимація називається лінійною. В результаті лінійного апроксимування одержують так звану лінію регресії (пряму). При  апроксимування називають квадратичним, а при  -кубічним.

Звичайно, апроксимування не обов'язково має бути поліноміальним. Наприклад, якщо відомо, що вимірювана функція є періодичною з відомим періодом 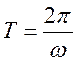, де - кругова частота, то за базові функції зручно використовувати таку сукупність:

; ; ;   .  .  .,

;      ;   .  .  .  ,

тобто використовувати апроксимацію у вигляді ряду Фур'є. Тут  є  цілим додатним числом, яке дорівнює номеру гармоніки у розкладі Фур'є.

Наведена сукупність функцій є ортогональною на інтервалі, кратному періодові . Тому застосування її є вельми ефективним (потребує мінімуму обчислень), якщо інтервал вимірювання обрати кратним періодові.

Опис результатів спостережень методом найменших квадратів ускладнюється, якщо невідомі коефіцієнти в рівняння регресії входять нелінійно. Однак у багатьох випадках задачу вдається спростити, застосовуючи деякі прості перетворення вихідного рівняння регресії.

Приклад.У ряді випадків до лінійної залежності можуть бути зведені експериментальні дані, коли їхній графік у декартовій системі координат не є пряма. Цього можна  досягти шляхом уведення нових змінних , які вибираються так, щоб точки  лежали на прямій. Таке перетворення називається вирівнюванням даних. Наприклад, рівняння регресії має вигляд х=ce. Прологарифмуємо функцію lnх=lnc+kt. Позначимо lnx=z, lnc=a. В результаті одержуємо лінійне рівняння z=a+kt. Методом найменших квадратів знаходимо значення а і k (див. приклад вище), після чого визначимо так само c=e

Вибір вигляду регресійної залежності можна здійснити за таблицею. Для цього за вихідними даними обчислюють середні значення х_ср та у_ср

,  ,  ,

  .

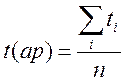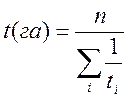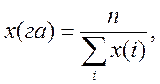
Величина обчислюється в такий спосіб:

1) якщо  збігається з одним із вихідних , то ;

2) якщо  знаходиться між  і , то  знаходимо як ординату відповідної точки на відрізку прямої, що з'єднує вузли  і, за формулою

.

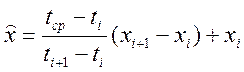Вибір рівняння регресії здійснюється шляхом пошуку мінімального значення виразу 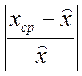 і відповідної йому функції, використовуючи таблицю.

Таблиця 5.1 Вибір залежності

N	.					Вигляд  функції
1	t(ар)	x(ар)				x=а0+a1*t
2	t(га)	x(ар)				x=а0+а1 /t
3	t(ге)	x(ар)				x=a0+a1 lg t
4	t(ар)	x(ге)				x=a0*a1t
5	t(ге)	x(ге)				x=a0*ta1
6	t(га)	x(ге)				x=exp(a0+a1 /t)
7	t(ар)	x(га)				x=1/(a0+a1*t)
8	t(ге)	x(га)				x=1/(a0+a1 lg t)
9	t(га)	x(га)				x=t/(a0+a1*t)

Таблицею доречно користуватися, якщо значення нашої функції носять монотонний характер.