Проблемні питання сучасної асиметричної криптографії та можливі шляхи їх вирішення, страница 7

То есть,  действительно отображает любые две точки из  в подгруппу -ых корней из единицы мультипликативной группы поля [6]. 

Пример 1: Из примера  [1] видно, что для эллиптической кривой  над полем  , точки  и  являются линейно-независимыми точками 2-го порядка кручения, где . Вычислим спаривание Вейля, то есть, вычислим  , используя значения дивизоров  и .

1.  Пусть  и . Здесь , а точка  является случайно выбранной точкой на кривой [1,2].

Построим функцию , которая удовлетворяет условию . Заметим, что линия, касательная к точке второго порядка кручения , является вертикальной линией . Так как  [1,3], то мы получим что .

Далее, построим функцию , которая удовлетворяет условию

.        (3)

Применив для вычисления (3) правило (36) из [1] получаем

,

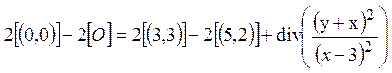где  это наклонная линия, которая пересекает точки  и . Уравнение  задает вертикальную линию, которая пересекает точку . Далее учтем  что линия, касательная для точки  2-кручения, это вертикальная линия . Используя выражение (19) из [1] получим, что . В результате имеем

.

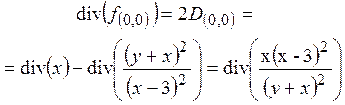Затем оценим  следующим образом [1,2]:

.

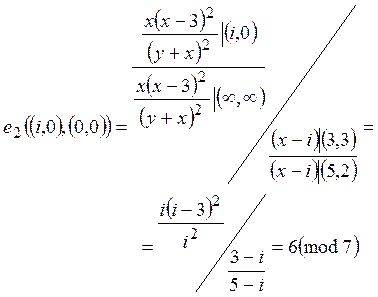Число 6 это корень квадратный из 1 по модулю 7, так как . Отметим, что 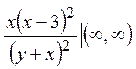 стремится к единице. Рост дроби определяется отношением ; эта дробь принимает на кривой в точке на бесконечности значение 1, так как уравнение нашей кривой    .

2.  Пусть  и  остаются неизменными, и пусть функция  будет образована на основе  , которая использует другую точку . Например, пусть . Тогда , так как в этом случае . Используя предыдущий пример, получаем

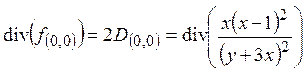
В этом случае для вычисления спаривания можно использовать выражение

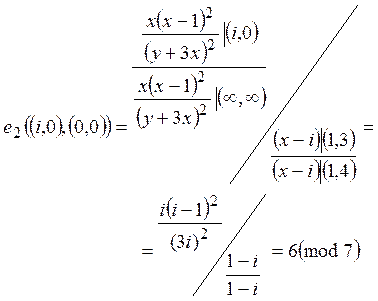
12.6 Основні історичні етапи криптографії на базі спарювання.

          Галузь еліптичних кривих вивчається вже достатньо давно не тільки криптографічним співтовариством але й багатьма математиками світу. Практичне значення в сучасній криптографії та значний інтерес зі сторони криптографічного співтовариства еліптичні криві над кінцевими полями знайшли у 1985 році. Koblitz[] та Miller[] незалежно один від одного представили реалізацію криптографічної системи на базі дискретного алгоритму в групах точок еліптичної кривій з більш вигідними показниками безпеки в порівнянні з мультиплікативними групами над кінцевими полями. 

Найбільш поширені на сучасний день спарювання Вейля та Тейта на еліптичних кривих математики вивчали вже давно, та визначили багато властивостей, серед яких найбільш важливими для криптографії є білінійність. У 1993 році Menezes у своїй роботі[] (MOV сведення)  показав, що є можливість використання спарювання Вейля для атаки на криптографічні  системи які базуються на вирішенні проблеми дискретного логарифма.  Вже 1994 році Frey та Ruck (FR сведення) показали[], що для атак на еліптичні криві може використовуватися також і спарювання Тейта. 

У 2000 році Sakai[] та Joux[] незалежно один від одного  запропонували оригінальне та просто вирішення використання спарювання в якості будівничого елементу при створенні нових криптографічних систем. Так Joux представив аналог протоколу Діффі-Гелмана який давав можливість декільком сторонам визначати спільний секрет. Sakai же в своїй роботі вивчав деякі аспекти використання спарювання в криптографії на базі ідентифікаторів. Тут треба сказати, що ідею побудування та базові принципи криптографічних  систем на базі ідентифікаторів   були закладені Shamir[] у 1984 році. В таких системах відкритий ключ в ІВК напряму зв’язаний з ідентифікаційною інформацією самого власника. Деякі варіанти цифрового підпису (серед них і варіан який представив Shamir[]) на базі ідентифікаторів були відомі, ще до 2000 року. Але варіанти шифрування та розподілення ключів були представлені вже після 2001 року.

Роботи Sakai[] та Joux[] дали значний поштовх у розвитку систем на базі ідентифікаторів. Так у 2001 році Cocks[] та Boneh-Franklin[] незалежно один від одного запропонували схеми шифрування на базі ідентифікаторів. Згодом з терміном практично в один місяць представлялися нові протоколи на базі ідентифікаторів яки використовували спарювання Тейта та Вейля (,,,,,, 10 – 12 посилань). Для бажаючих ознайомитися зі всіма сучасними додатками на базі ідентифікаторів пропонуємо звернутися до Pairing-BasedCryptoLounge[] одного з авторів систем на базі ідентифікаторів.