Оцінка складністі алгоритмів факторизації. Факторизація великих цілих чисел (Практичне заняття № 2), страница 2

 Слід звернути увагу, що ми відразу вдало підібрали многочлен, при якому метод швидко дав результат. Це буває не завжди.

 Щоб оцінити середній час роботи даного алгоритму, розглянемо більш простій для аналізу, але менш ефективний алгоритм, що відрізняється від алгоритму 1 тим, що на кроці 3 обчислюється НСД для всіх пар чисел,   Назвемо його алгоритмом 2.

 Скористаємося відомим „ парадоксом днів народження „.

 Теорема.  Хай     для випадкової вибірки з   елементів об'єму , де , вірогідність того, що всі елементи у вибірці будуть попарно різними, допускає наступну оцінку зверху:

.

Доведення. Маємо

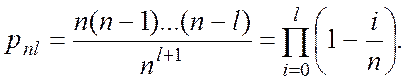
Переходячи до логарифмів і враховуючи, що  за  отримуємо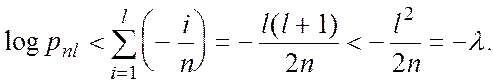

Теорема доведена.

 У нашому випадку розглядатимемо послідовність   як випадкову вибірку. Для випадкового відображення   це виправдано. Хоча многочлен , звичайно, не можна розглядати як випадкове відображення, проте, практичні результати говорять про хорошу відповідність приведених нижче оцінок трудомісткості з тими, які виходять насправді.

 Хай  - нетривіальний дільник числа . Тоді умова  рівносильна умові   або . Тому, застосовуючи доведену вище теорему для вибірки, зформованої послідовністю  де  одержуємо, що при   вірогідність існування пари  такої, що , буде не менший, ніж .

 Оскільки  , то вірогідність одночасного виконання рівності  буде мала, і можна вважати, що , і дана пара дозволяє факторизувати число .

 Таким чином для знаходження даної пари з надійністю  необхідно обчислювати   знаків послідовності, , де . Звідси середня складність алгоритму 2 оцінюється величиною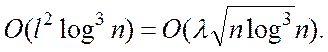 

 Перейдемо тепер до розгляду алгоритму 1. Зауважимо, що оскільки - многочлен над ,  то для будь-якого дільника  числа  і будь-якої пари   з умовою   виконуватимуться і порівняння  і т.д.

 Хай алгоритму 2 для знаходження пари   з умовою   необхідна послідовність довжини . Покажемо, що в даному випадку алгоритм 1 дозволяє знайти пару  з умовою  , де   при деякому , де   - пара, знайдена алгоритмом 2, така, що . Хай число   має в своєму двійковому записі   біт, тобто . Тоді при  число   знаходитиметься в інтервалі , оскільки ,

 причому, так як , то

 Таким чином, якщо другому алгоритму буде потрібно послідовність довжини , то першому алгоритму необхідна послідовність довжини . При цьому складність першого алгоритму оцінюється вже величиною , що набагато краще, ніж  Тим самим доведена теорема.

 Теорема. Хай  - складене число. Існує константа С така, що для будь-якого позитивного числа   вірогідність події, що полягає в тому, що   метод Полларда не знайде нетривіального дільника за час , не перевершує величини  .

Алгоритм Полларда- Штрассена.

 Алгоритм Полларда- Штрассена є детермінованим алгоритмом для знаходження мінімального простого дільника і має оцінку складності  Він заснований на наступній теоремі.

 Теорема. Хай   , . Тоді для будь-якого   найменший простий дільник числа   може бути знайдений за   двійкових операцій.

 Доказ. Згрупуємо співмножники у виразі

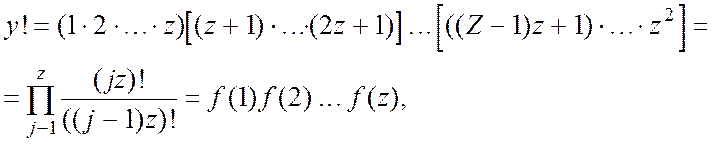
де

Тому для знаходження найменшого простого дільника числа  можна скористатися наступним способом:

 Крок 1. Обчислюємо значення

 Крок 2. Обчислюємо  до отримання першого нетривіального дільника.

 Крок 3. Послідовно здійснюємо пробні ділення  на числа  Перше число з цього інтервалу, що ділить без  залишку   очевидно, і буде мінімальним простим дільником числа .

Оцінимо тепер складність кожного кроку. Для виконання першого кроку знайдемо коефіцієнти многочлена

  Скористаємося алгоритмом швидкого дискретного перетворення Фурье і послідовно знайдемо  добутків многочленів першого ступеня, потім  добутків многочленів другого ступеня, і т.д. У результаті виходить

 

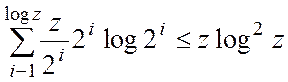
 арифметичних операцій. При його виконанні необхідно виконувати операції складання і множення цілих чисел. Зауважимо, що нам досить знати значення   Як операції тут виступають множення і ділення із залишком, що мають складність   Тому, складність знаходження коефіцієнтів многочлена дорівнює ).

 Обчислення значень тепер виконується за тією ж схемою, тільки у якості лінійних співмножників виступають многочлени  Тому складність першого етапу рівна