Задача 3.
“Парадокс” днів народження. Ця задача може бути сформульована таким чином. Чому дорівнює мінімальне значення k, при якому ймовірність того, що, у крайній мірі, у двох осіб із групи в k осіб дні народження співпадуть, буде Рз.
Розв’язок задачі здійснити без урахування 29 лютого при умові, що кожний день народження рівноймовірний.
Розв’язок задачі:
Введемо ймовірність ![]() та
знайдемо ймовірність того, що в групі із k осіб дні народження не співпадуть, позначивши
її як
та
знайдемо ймовірність того, що в групі із k осіб дні народження не співпадуть, позначивши
її як ![]() . Зрозуміло,
що:
. Зрозуміло,
що:
![]() ,
,
тому
![]() .
.
Зрозуміло також, що k![]() 365.
365.
Знайдемо число різних способів N, якими можна отримати k значень без повторень. Для першого елемента ми маємо
365 значень без повторень, для другого 364, які залишилися, і так далі.
Тому загальне число підходящих
способів
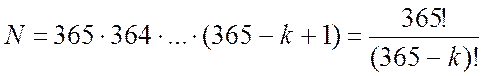 .
.
Якщо виключити умову відсутності співпадань днів народження, то кожний елемент (подія) може набувати будь-якого із 365 можливих значень. Загальна сума можливих подій дорівнює 365k. Тому ймовірність відсутності співпадань дорівнює відношенню числа варіантів без співпадань до загального числа варіантів.
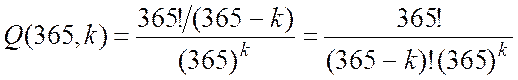 . (1.175)
. (1.175)
Тому
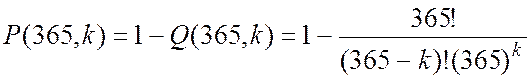 .
.
В таблиці 1.9 наведено наближені значення P(365,k).
k |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
P |
0,13 |
0,4 |
0,71 |
0,89 |
0,97 |
0,99 |
0,999 |
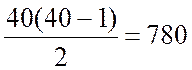 різних пар,
різних пар,
тому й імовірність для k=40 в таблиці достатньо велика.
Задача 4.
Нехай є деяка функція хешування h=H(M), де М – інформація довільної довжини, причому h може приймати n=2m значень. Скільки випадкових повідомлень k треба подати на вхід перетворювача Н, щоб відбулося з ймовірністю Рз хоча б одне співпадання вигляду
![]() ,
,
тобто відбулася колізія.
Розв’язок задачі:
Розв’язок задачі ґрунтується на “парадоксі” про день народження (див. Задача 3). Але ця задача носить більш загальний характер.
У нашому випадку є цілочислова випадкова величина з
рівноймовірним розподілом значень від 1 до n, та є вибірка із k
значень випадкової величини (![]() ).
Знайдемо ймовірність P(n,k) того, що серед значень H(M) у
виборці, у крайньому випадку, дві співпадають
).
Знайдемо ймовірність P(n,k) того, що серед значень H(M) у
виборці, у крайньому випадку, дві співпадають
![]() . (1.176)
. (1.176)
Використовуючи підхід, викладений вище під час розв’язку задачі 3, отримаємо узагальнення виразу (1.175)
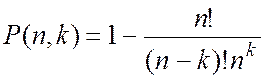 . (1.177)
. (1.177)
Для спрощення розрахунків вираз (1.177) можна спростити. Для цього використовуємо те, що справедливо
![]() , для усіх
, для усіх ![]() .
(1.178)
.
(1.178)
Крім того, при малих значеннях х (наприклад, ![]() ) можна вважати, що:
) можна вважати, що:
![]() .
(1.179)
.
(1.179)
Далі запишемо (1.177) у вигляді:
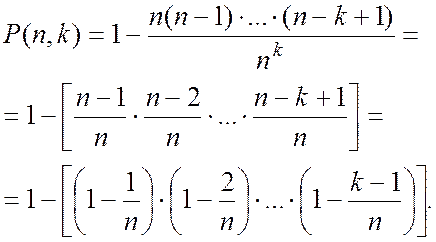 (1.180)
(1.180)
Оскільки в нашому випадку 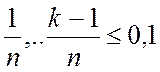 , то
зробимо в (1.180) заміну, використовуючи (1.178).
, то
зробимо в (1.180) заміну, використовуючи (1.178).
У результаті маємо
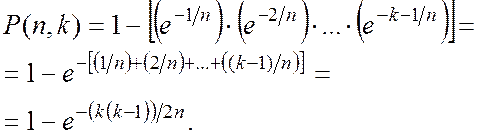 (1.181)
(1.181)
Розв’язок можна отримати, розв’язавши (1.181)
![]() , так як Рз
відомо. Оскільки реально Рз
, так як Рз
відомо. Оскільки реально Рз![]() 1,
1,
то
![]()
![]()
або
![]() ,
,
і далі
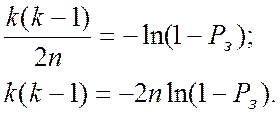
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.