Обчислюємо
значення ![]()
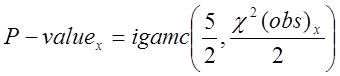 . (50)
. (50)
Значення
![]() для кожного x має бути більше від 0.01.
для кожного x має бути більше від 0.01.
Рекомендована
довжина послідовності: ![]() .
.
Примітка
. На справді, стан x має приймати значення від ![]() до
до ![]() . Розробники керівництва НІСТ, вибрали іншу
формулу, виграли у простоті, але програли (хоча зовсім не багато) у точності.
. Розробники керівництва НІСТ, вибрали іншу
формулу, виграли у простоті, але програли (хоча зовсім не багато) у точності.
3.16. Перевірка випадкових відхилень-2 (Random Excursions Variant Test)
Даний тест є розширенням попереднього.
Нехай
![]() - двійкова послідовність довжини n.
Перетворимо її у послідовність Х:
- двійкова послідовність довжини n.
Перетворимо її у послідовність Х: ![]() (тобто 1®1, 0 ® -1). Cформуємо
послідовність:
(тобто 1®1, 0 ® -1). Cформуємо
послідовність:
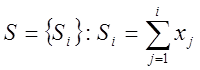 . (51)
. (51)
Cформуємо послідовність:
![]() (52)
(52)
Розіб’ємо
її на блоки, що мають вигляд ![]() , тобто на послідовності,
у яких перший та останній елементи дорівнюють нулю, а всі інші відмінні від
нуля.
, тобто на послідовності,
у яких перший та останній елементи дорівнюють нулю, а всі інші відмінні від
нуля.
Будемо
вважати, що стан будь якого не нульового елементу х блоку може приймати
одно із значень : (-9), (-8), (-7),...8, 9, тобто ![]() .
.
Нехай
J – загальна кількість блоків та ![]() -
кількість появ станів х у всіх J блоках.
-
кількість появ станів х у всіх J блоках.
Обчислюємо
значення ![]() для кожного х
для кожного х
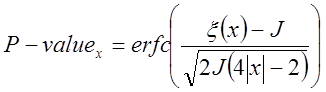 . (53)
. (53)
Значення
![]() для кожного x має бути більше від 0.01.
для кожного x має бути більше від 0.01.
Рекомендована
довжина послідовності: ![]() .
.
Примітка
. Як і у попередньому тесті розробники керівництва НІСТ спростили значення x.
На справді, стан x має приймати значення від ![]() до
до ![]() .
.
4. Математичне обґрунтування тестів
4.1.Частотний тест
Основною ідеєю тесту є використання нульової гіпотези: у
послідовності незалежних випадкових величин з розподілом Бернуллі (Х чи ε,
де Х = 2ε – 1, так що Sn = X1
+ … + Xn = 2(ε1 + … + εn)
- n) імовірність появи 1 складає ½. Відповідно до класичної теореми
Лапласа, для досить великого числа іспитів розподіл біноміальної суми,
нормалізованої по ![]() , близько наближений до
стандартного нормального розподілу. Даний тест використовує апроксимацію оцінки
близькості частки 1 до ½. Результати всіх наступних тестів спираються на
результати проходження цього основного тесту.
, близько наближений до
стандартного нормального розподілу. Даний тест використовує апроксимацію оцінки
близькості частки 1 до ½. Результати всіх наступних тестів спираються на
результати проходження цього основного тесту.
Даний тест отриманий з центральної граничної теореми для випадкового блукання, Sn = X1 + … + Xn... Відповідно до центральної граничної теореми,
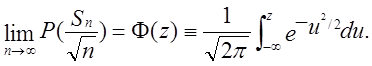 (54)
(54)
Цей класичний результат є основою для найпростішого тесту на випадковість. Це припускає, що для позитивного z
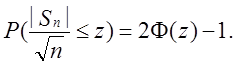
Відповідно до тесту, заснованому на статистиці ![]() , обчислюється розглянута величина |s(obs)|
= |X1 + … + Xn| /
, обчислюється розглянута величина |s(obs)|
= |X1 + … + Xn| /![]() ,
після чого рахується відповідна Р-величина, рівна
,
після чого рахується відповідна Р-величина, рівна ![]() . Тут erfc є (додатковою) функцією
помилки
. Тут erfc є (додатковою) функцією
помилки
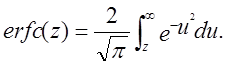
Приклад.
Вхід: e = 110010010000111111011010101000100010000101101000110
0001000110100110001001100011001100010100010111000,
n = 100.
Тест:
s100 = n1 – n0 = 42 – 58 = -16,
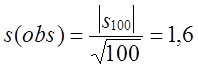 ,
,
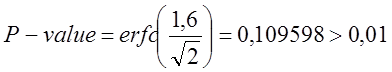 - тест пройдений.
- тест пройдений.
4.2.Частотний тест в середині блоку
Метою тесту є виявлення відхилень частки «1» від ½
усередині під послідовностей, що не перекриваються, на які розбивається вхідна
послідовність. Для оцінки відхилення використовується критерій ![]() .
.
Малі P - значення вказують на великі відхилення від рівної пропорції одиниць і нулів принаймні в одному з блоків. Рядок 0 і 1 (чи 1 і -1) розділений на множину непересічних блоків. Для кожного блоку обчислюється пропорція одиниць. Статистика хі-квадрат порівнює пропорції блоку з ідеалом ½. Статистика заснована на розподілі хі-квадрат зі ступенями свободи, рівними кількості блоків.
Параметрами цього тесту є М і N, так що n
= МС, тобто, послідовність розбивається на N блоків, кожен
довжиною М. Для кожного з цих блоків імовірність появи «1» оцінюється
шляхом спостереження відповідних частот «1», ![]() , і
= 1, ..., N. Сума
, і
= 1, ..., N. Сума
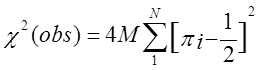
у припущенні гіпотези випадковості повинна мати розподіл ![]() з N ступенями свободи. Р-значення
розраховується відповідно до вираження
з N ступенями свободи. Р-значення
розраховується відповідно до вираження
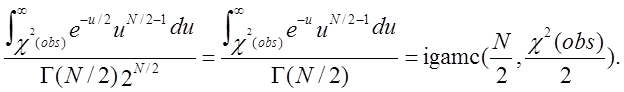
Приклад.
Вхід: e = 110010010000111111011010101000100010000101101000110
0001000110100110001001100011001100010100010111000,
n=100,
M=10.
Тест:
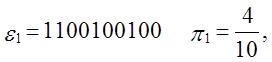
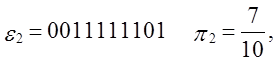
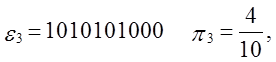
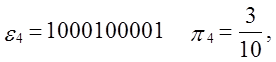
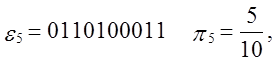
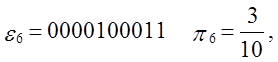
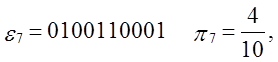
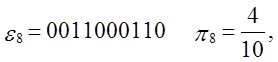
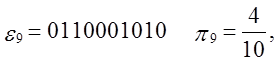
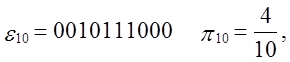
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.