Методика статистичного тестування: Технічний звіт ІІТ – 001-2004, страница 17

Таким чином,  є статистикою типу χ², але це розповсюджена помилка думати, що  має χ²-розподіл. Насправді частоти  не є незалежними.

Відповідна узагальнена послідовна статистика для тестування випадковості [12], [14], [15]:

і                                                         

(Тут = =0.) Тоді  має χ²-розподіл з 2^m-1 ступенями свободи,  має χ²-розподіл з 2^m-2 ступенями свободи. Таким чином, для малих значень m, , можна знайти відповідні 2m Р-значень за допомогою стандартних формул.

Результат для  і звичайний підрахунок частот даний некоректно в [12] стор.81, формула (5.2): +1 повинна бути замінена на –1.

Збіжність  до χ²-розподілу доведена в [2].

Приклад.

Вхід:

e = 0011011101,

n = 10,

m = 3.

Тест:

m = 3:

              e' = 001101110100,

              v₀₀₀ = 0, v₀₀₁ = 1, v₀₁₀ = 1, v₀₁₁ = 2, v₁₀₀ = 1, v₁₀₁ = 2, v₁₁₀ = 2, v₁₁₁ =1;

m = 2:

              e' = 00110111010,

              v₀₀ = 1, v₀₁ = 3, v₁₀ = 3, v₁₁ = 3;

m = 1:

              e' = 0011011101,

              v₀ = 4, v₁ = 6;

         

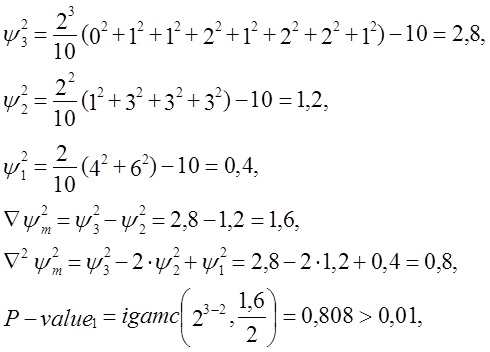
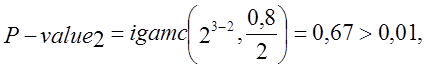-тест пройдено.

4.13. Ентропійний тест

Ентропійні характеристики [16] базуються на повторенні шаблонів у рядку. Якщо Y_i(m) = (ε₁, …, ε_{i + m - 1}), встановлюються

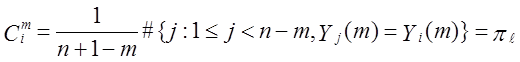
і

 ,

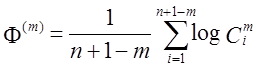де - відносна частота входжень шаблона Y_i(m) у строку, і  - ентропія емпіричного розподілу, яка виникає з безлічі всіх 2^m можливих шаблонів довжини m,

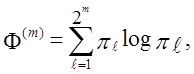
де - відносна частота шаблону ℓ = (i₁, …, i_m) у строці.

Ентропія ApEn порядку m, m ≥ 1, визначається як

ApEn(m) =  -

з ApEn(0) = - . Згідно [16], “ApEn(m) вимірює логарифмічну частоту, з якою блоки довжини m, обмежені разом, залишаються обмеженими разом для блоків, поповнених однією позицією. Таким чином, малі значення ApEn(m) вказують на  строгу регулярність, чи постійність, у послідовності. І навпаки, великі значення ApEn(m) вказують на істотне коливання (нестійкість), чи нерегулярність”.

У [17] послідовність називається m – нерегулярною (m - випадковою), якщо ентропія ApEn(m) приймає найбільше можливе значення. Тут розраховувалися величини ApEn(m), m = 0, 1, 2 для двійкових і десяткових розширень е, π, ,  з несподіваним результатом, що полягає в тім, що розширення  демонструє більшу нерегулярність, чим π.

Для фіксованого блоку довжиною m передбачається, що в довгих випадковим (нерегулярних) рядках ApEn(m) ~ log 2. Обмежуючий розподіл n[log2 - ApEn(m)] збігається з χ²-випадковою перемінною з 2^m ступенями свободи. Даний факт складає основу тесту [18].

Таким чином, при χ²(obs) = n[log2 – ApEn(m)], звітним Р-значенням є

igamc (2^m-1, χ²(obs) / 2).

Насправді, це обмежуюче розподілення ентропії більш точно для модифікованого визначення

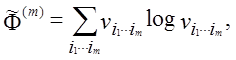
де  позначає відносну частоту шаблона (i₁, …, i_m) у поповненій (чи циклічній) версії вихідної строки, тобто в строці (ε₁, …, ε_n, ε₁, …, ε_{m - 1}). Нехай - частота шаблона i₁, …, i_m. Відповідно до нашого визначення, 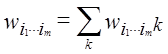, так що для будь-якого m, .

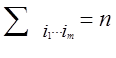Визначимо модифіковану ентропію як

 =  - .

Згідно нерівності Дженсена,  для будь-якого m, оскільки можливо, що log s < ApEn(m). Отже, найбільше можливе значення модифікованої ентропії є просто log s, що досягається при n = s^m, і розподіл усіх m-шаблонів є рівномірним. Коли обчислюється ентропія для декількох значень m, дуже зручно мати суму всіх частот m-шаблонів, еквівалентних n.

Коли n велико, ApEn(m) і його модифікована версія не можуть сильно відрізнятися. Дійсно, при

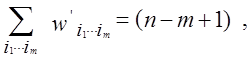
і  З цього випливає, що

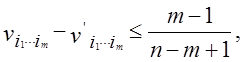
і наводить на думку, що для фіксованих m,  і  повинні бути обмежені для великих n. Отже, ентропія [17] і її модифікована версія також є обмеженими, і їхні асимптотичні розподіли повинні збігатися.

Приклад.

Вхід:

e = 0100110101,

n = 10,

m = 3.

Тест:

m = 3:

              e' = 010011010101,

              #000 = 0, #001 = 1, #010 = 3, #011 = 1, #100 = 1, #101 = 3, #110 = 1, #111 = 0;

            

             j⁽³⁾ = 0×ln0 + 0,1×ln0,1 + 0,3×ln0,3 + 0,1×ln0,1 + 0,1×ln0,1 + 0,3×ln0,3 + 0,1×ln0,1 + 0×ln0 = - 1,6434;

m = 4: