Асимптотичний
розподіл ![]() уздовж послідовності парних і непарних
значень n є дискретною випадковою величиною, обчисленої шляхом
змішування двох геометричних випадкових величин (одна з яких має негативне
значення). Строго говорячи, асимптотичного розподілу як такого не існує.
Випадки з n парним і n непарним повинні бути очищені розділом із
двома різними розподілами.
уздовж послідовності парних і непарних
значень n є дискретною випадковою величиною, обчисленої шляхом
змішування двох геометричних випадкових величин (одна з яких має негативне
значення). Строго говорячи, асимптотичного розподілу як такого не існує.
Випадки з n парним і n непарним повинні бути очищені розділом із
двома різними розподілами.
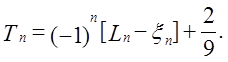 (58)
(58)
Тут
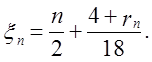 (59)
(59)
Дана статистика, що приймає тільки цілочисельне значення, прагне в розподілі до випадкової величини Т. Цей обмежувальний розподіл асиметричне вправо. Поки Р(Т = 0) = 1/2, для k = 1, 2, …
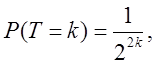 (60)
(60)
для k = -1, -2, …
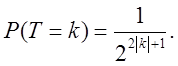 (61)
(61)
З (60) випливає
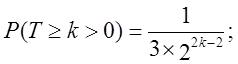
для k < 0 з (61) випливає
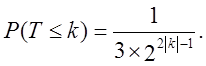
Таким чином, Р-значення відповідної розглянутої величини Tobs може бути розраховано наступним шляхом. Нехай k = [ | Tobs | ] + 1. Тоді Р-значення дорівнює
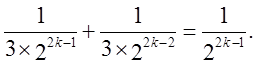
При розгляді дискретної сутності даного розподілу і неможливості досягнення рівномірного розподілу для Р-значення, можуть бути використані деякі стратегії, використовувані з іншими тестами в даній ситуації. А саме, розбивка строки довжиною n, такою, що n = MN, на N підстрок, кожна довжиною M. Для тесту, заснованого на статистиці лінійної складності (58), рахується ТМ j-ої підстроки розміром М, і вибираються К+1 класів (у залежності від М). Для кожної з цих підстрок визначаються частоти v0, v1, …, vДо значень ТМ , що належать кожному з К+1 обраних класів v0, v1, …, vК = N.
Теоретичні імовірності π0, π1, …, πДо даних класів визначаються з (60) і (61). Для цього М повинно перевищувати 500. Рекомендується вибирати М з інтервалу 500 ≤ М ≤ 5000.
Частоти сполучаються χ2 – статистикою
 ,
,
що, відповідно до гіпотези випадковості, має приблизно χ2 – розподіл з К ступенями свободи. Р-значення обчислюється як

Обмежувальна умова для використання χ2 – апроксимації:
![]()
Для прийнятно великих значень M і N наступні класи (К = 6) є адекватними: { T ≤ -2,5 }, {-2,5 < T ≤ -1,5 }, {-1,5 < T ≤ -0,5 }, {-0,5 < T ≤ 0,5 }, {0,5 < T ≤ 1,5 }, {1,5 < T ≤ 2,5 } і {T > 2,5 }.
Імовірності цих класів π0 = 0,01047, π1 = 0,03125, π2 = 0,12500, π3 = 0,50000, π4 = 0,25000, π5 = 0,06250, π6 = 0,020833. Дані імовірності є здебільшого відмінними від імовірностей, обчислених з нормальної апроксимації, для яких їхні значення відповідно є: 0,0041, 0,0432. 0,1944, 0,3646, 0,2863, 0,0939, 0,0135.
Приклад.
Вхід:
e = 1101011110001,
n = 13,
M = 13,
N = 1.
Тест:
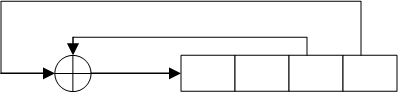
Мінімальна довжина ЛРР, необхідного для генерації даної послідовності, дорівнює 4 (рис.2), тобто L1 = 4.
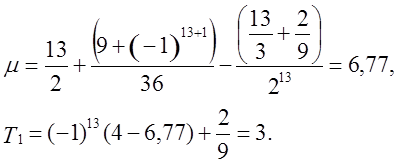
 |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
|
... |
Рис.2. ЛРР довжиною 4, який формує послідовність e
Розклад на категорії виконано наступним чином:
якщо Ti £ -2, v0 збільшуємо на 1,
якщо –2 < Ti £ -1, v1 збільшуємо на 1,
якщо –1 < Ti £ 1, v2 збільшуємо на 1,
якщо 1 < Ti £ 2, v3 збільшуємо на 1,
якщо Ti > 2, v4 збільшуємо на 1.
Таким чином, маємо v0 = 0, v1 = 0, v2 = 0, v3 = 0, v4 = 1.
Наступні ймовірності дорівнюють:
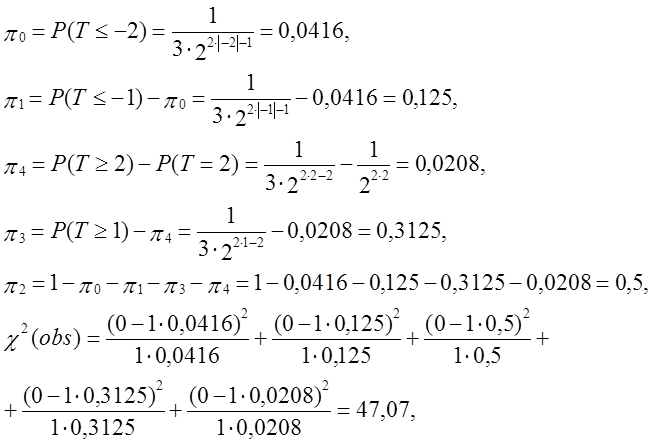
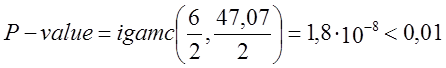 - тест не пройдено
- тест не пройдено
4.12. Послідовний тест
Тест серій (узагальнений) представлений комплектом процедур, заснованих на тестуванні рівномірно розподілених шаблонів заданої довжини.
Більш точно, для i1, …, im, які
пробігають через безліч усіх 2m можливих 0, 1 векторів
довжини m, нехай ![]() позначає частоту появи
шаблона (i1, …, im) у рядку біт (ε1,
…, εn, ε1, …, εm - 1).
позначає частоту появи
шаблона (i1, …, im) у рядку біт (ε1,
…, εn, ε1, …, εm - 1).
Установлюється
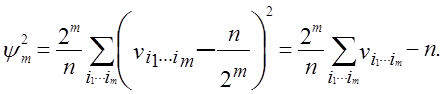
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.