Информатика и выч. техника \ Основы теории защиты информации

Криптоперетворення в групі точок еліптичних кривих, страница 6

Точка не належить до і не є розв’язанням рівняння (А.3.1). Набір точок на кривій типу називається афінним поданням кривої.

А.3.2.1.1 Груповий закон в афінному поданні

Для еліптичної кривої над полем введено бінарну операцію :, яка дозволяє для двох точок кривої обчислити третю точку на кривій . Множина точок еліптичної кривої є абелевою групою у відношенні до операції додавання , що має такі властивості:

- точка нескінченності для групової операції на кривій є нейтральним елементом, тобто , для всіх точок кривої ;

- якщо точка є афінним поданням на кривій , тоді зворотна точка має координати та ;

- якщо точки та є афінними точками кривої , причому , тоді координати точки суми визначаються такими формулами:

;

, (А.3.2)

причому

, якщо , (А.3.3)

або

, якщо . (А.3.4)

Із (А.1.1) та (А.3.1) випливає, що обчислення суми та подвоєння точок еліптичних кривих над полями та здійснюється за одними й тими ж формулами. Відмінність в тому, що для операції виконуються за модулем , а для за модулем -значного полінома . Основним недоліком афінного подання є значна складність операцій додавання та подвоєння. Зменшення складності досягається за рахунок використання проективних координат.

А.3.2.2 Проективне подання

Проективне подання операцій в групі точок еліптичних кривих над скінченним простим полем наводиться нижче. При проективному поданні для виконання операцій додавання та подвоєння збільшується число множень, але завдяки відсутності операції ділення за модулем складність операції в цілому зменшується.

А.3.2.2.1 Проективні площини над полем

Розглянемо набір точок , що складається із усіх можливих значень трійок над полем , крім трійки . Введемо для цієї множини відношення еквівалентності, яке позначимо символом “~”. Це відношення еквівалентності має такі властивості: , тобто існує , таке що та .

Проективна площина над полем є набором еквівалентних класів, які визначаються операцією . Еквівалентний клас, якому відповідає трійка позначається як . Цей еквівалентний клас називається точкою проективних координат над полем . Причому точка не належить проективній площині .

А.3.2.2.2 Проективне подання еліптичної кривої над полем

Аналогом афінного рівняння еліптичної кривої (А.3.1) в проективному поданні є кубічне рівняння

, (А.3.5)

де .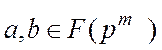

Еліптичні криві у проективному поданні складаються з усіх точок проективної площини , таких, що кожна трійка є розв’язком рівняння (А.3.5). Існує взаємно однозначне співвідношення між точками на кривій , коли крива визначена в афінному поданні, та точками в проективному поданні. Для афінного та проективного подання мають виконуватись такі умови:

- якщо є точкою в афінному поданні на кривій , тоді точка є відповідною точкою в проективному поданні;

- якщо з є розв’язком (А.3.5), тоді є однозначно відповідною точкою на кривій в афінному поданні;

- існує тільки одне розв’язання (А.3.5) з , яким є точка . Ця точка відповідає точці нескінченності .

А.3.2.2.3 Груповий закон у проективному поданні

При проективному поданні кривої (А.3.5) точки кривої відповідають таким властивостям:

- точка є нейтральним елементом відносно операції ;

- нехай буде проективним представленням точки на кривій , тоді є точкою ;

- нехай та є двома різними точками на кривій , причому обидві не рівні , тоді їх сума позначається як точка . Координати та точки обчислюються з використанням таких формул: