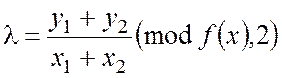 та
та 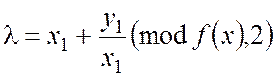 ,
,
або
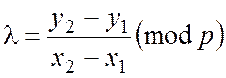 та
та
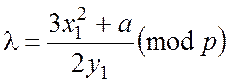 .
.
При цьому операція ділення заміняється знаходженням зворотного елемента, що є суттєво складною.
Особливістю криптографічних
перетворень в групі точок ЕК є те, що відкритий ключ обчислюється згідно з (6.1).
Якщо особистий ключ в
d сформовано випадково, а Q є відкритий ключ, то задача
криптоаналізу формулюється як знаходження особистого ключа d при відомих Q, G, а також ![]() .
.
6.4 Додаток А ОСНОВНА ІНФОРМАЦІЯ З ЕЛІПТИЧНИХ КРИВИХ
Метою даного додатка є подання математичних співвідношень, які необхідні для реалізації криптографічних перетворень з відкритими ключами та відкритим розповсюдженням ключів, що наводяться у цьому стандарті.
А.1 Скінченне просте поле ![]()
А.1.1 Визначення ![]()
Ми припускаємо, що читач добре ознайомлений з
модульною арифметикою. Як зазначено в розділі 4, для будь-яких простих ![]() існує скінченне поле, що складається точно
з
існує скінченне поле, що складається точно
з ![]() елементів. Це поле однозначно визначене з
точністю до ізоморфізму. У цьому документі розглядається як скінченне просте
поле
елементів. Це поле однозначно визначене з
точністю до ізоморфізму. У цьому документі розглядається як скінченне просте
поле ![]() . Для поля визначено дві операції, які
мають назви додавання і множення, а також виконуються такі умови:
. Для поля визначено дві операції, які
мають назви додавання і множення, а також виконуються такі умови:
- елементи
поля ![]() у відношенні до операції додавання
у відношенні до операції додавання ![]() є абелевою групою;
є абелевою групою;
- елементи
поля ![]() , позначається як
, позначається як ![]() ,
у відношенні до операції множення
,
у відношенні до операції множення ![]() є абелевою групою.
є абелевою групою.
Мультиплікативна частина простого поля без елемента ![]() позначається як
позначається як ![]() .
Вона є циклічною групою порядку
.
Вона є циклічною групою порядку ![]() . При цьому існує в
крайньому випадку один елемент
. При цьому існує в
крайньому випадку один елемент ![]() у групі
у групі ![]() такий, що кожний елемент
такий, що кожний елемент ![]() у групі
у групі ![]() може
бути однозначно записаний як
може
бути однозначно записаний як ![]() , де
, де ![]() .
.
Зворотній елемент групи ![]()
Нехай ![]() буде елементом групи
буде елементом групи ![]() . Тоді для кожного
. Тоді для кожного ![]() існує
існує ![]() такий, що
такий, що ![]() .
Елемент
.
Елемент ![]() називається мультиплікативно зворотнім до елемента
називається мультиплікативно зворотнім до елемента
![]() (інверсією), позначається як
(інверсією), позначається як ![]() , та може бути обчислений як
, та може бути обчислений як ![]() .
.
Характеристика скінченного поля
Якщо для досягнення нульового елемента необхідно ![]() додавань деякої точки
додавань деякої точки ![]() , то
, то ![]() називається
характеристикою поля. Якщо нульовий елемент не може бути досягнуто шляхом
додавання, тоді
називається
характеристикою поля. Якщо нульовий елемент не може бути досягнуто шляхом
додавання, тоді ![]() є нулем, а не нескінченним
елементом.
є нулем, а не нескінченним
елементом.
Ділення в полі ![]()
Значення ![]() в полі
в полі ![]() існує, якщо знаменник не нульовий. У цьому
випадку частка
існує, якщо знаменник не нульовий. У цьому
випадку частка ![]() .
.
Квадрати й не квадрати в полі![]()
Припустимо, що ![]() . Елемент
. Елемент
![]() називається квадратом у полі
називається квадратом у полі ![]() , якщо існує елемент
, якщо існує елемент ![]() такий, що
такий, що ![]() . Факт
існування квадратного кореня визначається за умови:
. Факт
існування квадратного кореня визначається за умови:
![]() є квадратом у полі
є квадратом у полі ![]() , якщо
, якщо ![]() .
.
Пошук квадратного кореня в полі ![]()
Для знаходження квадратних коренів у полі ![]() існують різні методи. Їх застосування
дозволяє для кожного
існують різні методи. Їх застосування
дозволяє для кожного ![]() знайти
знайти ![]() таке,
що
таке,
що ![]() , де
, де ![]() є
квадратом числа
є
квадратом числа ![]() . Приклади таких методів наведено
в [1] та [3].
. Приклади таких методів наведено
в [1] та [3].
А.1.2 Еліптичні криві над полем ![]()
У цій частині надаються два різних, але еквівалентних подання еліптичних кривих, що визначені над скінченними простими полями – афінне та проективне подання.
А.1.2.1 Афінне подання
Нехай ![]() буде скінченним простим
полем з
буде скінченним простим
полем з ![]() . Еліптична крива
. Еліптична крива ![]() над
полем
над
полем ![]() визначається несингулярним кубічним
рівнянням над полем
визначається несингулярним кубічним
рівнянням над полем ![]() . У цьому документі допускається,
що крива
. У цьому документі допускається,
що крива ![]() описана
«коротким рівнянням Вейєрштраса», тобто
описана
«коротким рівнянням Вейєрштраса», тобто
![]() , (А.1.1)
, (А.1.1)
з ![]() такими,
що виконується умова
такими,
що виконується умова ![]() у полі
у полі ![]() .
(Більш точно рівняння (А.1.1) називається афінним рівнянням Вейєрштраса).
.
(Більш точно рівняння (А.1.1) називається афінним рівнянням Вейєрштраса).
Еліптична крива ![]() над
полем
над
полем ![]() , що задається рівнянням виду (А.1.1)
складається з набору точок
, що задається рівнянням виду (А.1.1)
складається з набору точок ![]() таких, що виконується
рівняння
таких, що виконується
рівняння 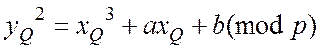 , для усіх цих точок разом з додатковою
точкою нескінченності
, для усіх цих точок разом з додатковою
точкою нескінченності ![]() .
.
Точка нескінченності ![]() не
міститься в
не
міститься в ![]() та не задовольняє рівняння (А.1.1). Набір
точок на кривій
та не задовольняє рівняння (А.1.1). Набір
точок на кривій ![]() вигляду
вигляду ![]() є
афінним поданням еліптичної кривої
є
афінним поданням еліптичної кривої ![]() .
.
А.1.2.1.1 Груповий закон в афінному поданні
Для точок еліптичної кривої визначено бінарну операцію
додавання ![]() :
: ![]() , яка
для кожної пари точок
, яка
для кожної пари точок ![]() , що належать кривій
, що належать кривій ![]() визначає третю точку
визначає третю точку ![]() . Еліптична крива
. Еліптична крива ![]() є
абелевою групою відносно операції
є
абелевою групою відносно операції ![]() та має такі
властивості.
та має такі
властивості.
Точка нескінченності ![]() є нейтральним
елементом для групової операції на кривій
є нейтральним
елементом для групової операції на кривій ![]() , тобто
, тобто ![]() , для всіх точок
, для всіх точок ![]() на
кривій
на
кривій ![]() .
.
Якщо точка ![]() є афінним поданням на кривій
є афінним поданням на кривій
![]() , тоді інверсна точка
, тоді інверсна точка ![]() має координати
має координати ![]() та
та ![]() .
.
Якщо точки ![]() та
та ![]() є афінним поданням точок на кривій
є афінним поданням точок на кривій ![]() , причому
, причому ![]() , тоді
координати
, тоді
координати ![]() суми
суми ![]() визначаються
відповідно до формул:
визначаються
відповідно до формул:
![]() ; (А.1.2)
; (А.1.2)
![]() . (А.1.3)
. (А.1.3)
При цьому, якщо ![]() , то
, то
![]() , (А.1.4)
, (А.1.4)
якщо ![]() , то
, то
![]() . (А.1.5)
. (А.1.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.