· великий розмір ансамблю послідовностей, формованих на одній алгоритмічній основі;
· оптимальність кореляційних функцій в ансамблі;
· збалансованість структури;
· максимальність періоду для даної довжини регістра зрушення.
ЛРР являє собою регістр зсуву зі зворотними зв'язками, об'єднаними за модулем 2. Його структурна схема представлена на рис. 1.
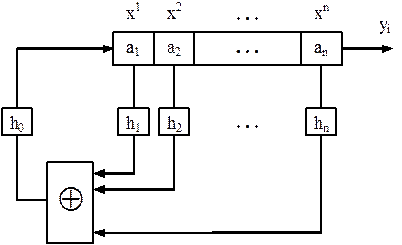
Рисунок 3.1
Чергове значення, яке формуються на виході ЛРР, обчислюється за формулою
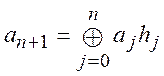 ,
,
де ![]() - операція обчислення
суми за модулем 2,
- операція обчислення
суми за модулем 2,
![]() - стан j - комірки ЛРР
- стан j - комірки ЛРР
![]() -
коефіцієнт зворотного зв’язку.
-
коефіцієнт зворотного зв’язку.
При цьому для двійкового ЛРР ![]() .
.
Кожному лінійному рекурентному регістру довжиною n розрядів можна зіставити поліном зворотних зв'язків h(x) із двійковими коефіцієнтами виду
![]() ,
,
причому обов'язково ![]() .
.
Якщо поліном h(x) – незвідний, то довжина послідовності, яка генерується ЛРР, максимальна і дорівнює
![]() .
.
Необхідно враховувати, що в чистому виді лінійні рекурентні послідовності не використовуються через низьку структурну скритність формованих ними послідовностей. Для підвищення структурної скритності використовують:
· комбінування декількох ЛРР;
· нелінійні функції в зворотному зв'язку регістра;
· нелінійну логіку і фільтрацію вмісту регістра.
Приклади незвідних поліномів (триномів)
|
x20 + x3 + 1 |
x41 + x20 + 1 |
|
x20 + x5 + 1 |
x41 + x3 + 1 |
|
x31 + x3 + 1 |
x52 + x7 + 1 |
|
x31 + x13 + 1 |
x52 + x21 + 1 |
|
Перевірити що поліном незвідний x3 + x1 + 1 |
X5 + x4 + 1 Перевірити що поліном незвідний |
Поліном ![]() є
примітивним, якщо він не зводиться, ділить поліном
є
примітивним, якщо він не зводиться, ділить поліном
![]() (10.7)
(10.7)
і не ділить всі поліноми ![]() , де
, де ![]() є
дільники
є
дільники ![]() , де n –
степінь полінома
, де n –
степінь полінома ![]() .
.![]()
Властивості ЛРП
1. Максимальна серія із n однакових символів „1” та максимальна серія із n-1 нулів.
2. Всі числа від 1 до ![]() з’являються
у деякій послідовності один раз(елементи поля на періоді з’являються один
раз).
з’являються
у деякій послідовності один раз(елементи поля на періоді з’являються один
раз).
Лінійно-рекурентний регістр забезпечує
формування послідовності з наперед відомим періодом ![]() . Якщо n=
257 , то
. Якщо n=
257 , то ![]() .
.
Твердження 1. Для розкриття закону формування лінійно-рекурентної послідовності необхідно і достатньо перехопити 2n поряд розміщених вірних бітів. Структурну скритність можна обчисли як:
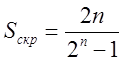 (10.8)
(10.8)
Лінійно-рекурентний регістр має низьку структурну скритність, але забезпечує необхідний гарантований період повторення .
2.9.1 Приклади розв’язку задач
Задача 1.
Визначити період повторення двійкової
послідовності, що формується за допомогою двох лінійних рекурентних регістрів
ЛРР1 та ЛРР2, якщо ЛРР1 та ЛРР2 реалізовані з використанням примітивних
поліномів ![]() та
та ![]() порядків
відповідно.
порядків
відповідно.
Розв’язок задачі.
Оскільки числа ![]() та 127
є прості числа Ейлера і періоди повторень
та 127
є прості числа Ейлера і періоди повторень ![]() та
та ![]() є також прості числа, то період повторення
L послідовності, що формується згідно з ЛРР1
є також прості числа, то період повторення
L послідовності, що формується згідно з ЛРР1 ![]() примітивний поліном) та ЛРР2
примітивний поліном) та ЛРР2 ![]() примітивний поліном)
примітивний поліном)
![]() .
.
Якщо ![]() і
і ![]() , то послідовність L може бути сформована з використанням схеми, що наведена на рис. 2.22.
, то послідовність L може бути сформована з використанням схеми, що наведена на рис. 2.22.
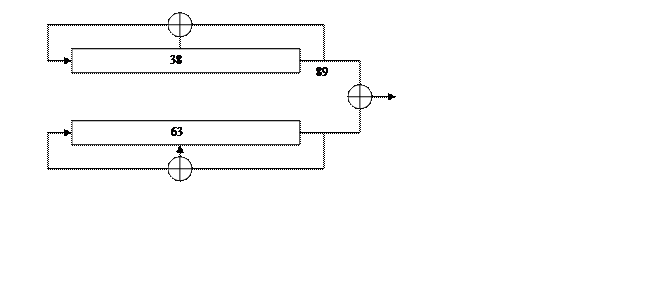
Рисунок 2.22 - Схема формування двійкової послідовності з періодом L
Задача 2.
Визначте закон формування гами скремблювання, якщо відомі відрізки послідовності
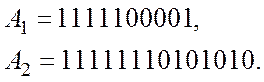
Покладемо спочатку, що ці послідовності сформовані
лінійним рекурентним регістром m-го порядку з поліномом ![]() (для А1) і, що перехоплено 2m символів. Значить для А1 m=5.
(для А1) і, що перехоплено 2m символів. Значить для А1 m=5.
Еквівалентна схема такого регістра наведена на рис. 2.23
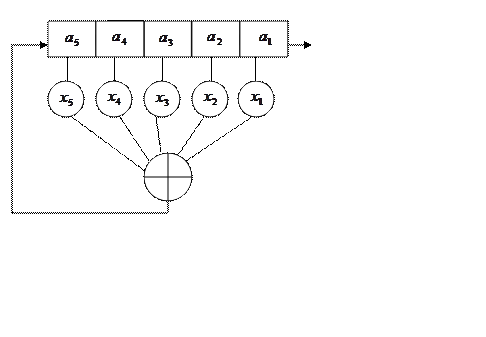
Рисунок 2.23 - Еквівалентна схема ЛРР з невідомим зворотним зв’язком
Присвоюючи вектору ![]() послідовно
значення 11111, 11110, 11100, 11000, 10000, отримаємо систему лінійних рівнянь
послідовно
значення 11111, 11110, 11100, 11000, 10000, отримаємо систему лінійних рівнянь
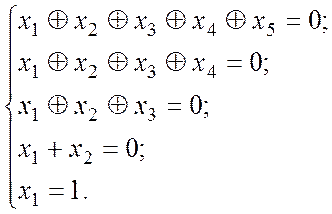
Цю систему можна розв’язати будь-яким методом,
враховуючи тільки, що ![]() і
і ![]()
Із системи зразу видно, що ![]() Далі,
підставивши
Далі,
підставивши ![]() в наступне рівняння, маємо
в наступне рівняння, маємо ![]()
Підставивши ![]() в третє рівняння,
маємо
в третє рівняння,
маємо ![]() значить
значить ![]()
Далі, підставивши ![]() в
четверте рівняння, маємо
в
четверте рівняння, маємо
![]() значить
значить ![]()
Підставивши в останнє рівняння, маємо
![]()
Таким чином, тільки ![]() і
і ![]() не є нульові, тому
не є нульові, тому ![]()
10.2.2 Конгруентний генератор:
Лінійний конгруентний генератор формує послідовність чисел відповідно до виразу
xi+1=(a xi+c)mod m, (10.10)
де a, c і m – цiло численні коефіцієнти.
Довжина періоду лінійної конгруентної послідовності залежить від вибору коефіцієнтів a, c і m. Довжина періоду дорівнює m тоді, коли
· c і m є взаємно простими числами;
· b = a-1 є кратним числу p для будь-якого простого p, що є дільником m;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.