














ЛЕКЦІЯ № 3.2 З ДИСЦИПЛІНИ
«ОСНОВИ ТЕОРІЇ ЗАХИСТУ ІНФОРМАЦІЇ»
Тема лекції
« ВСТУП В КРИПТОАНАЛІЗ RSA КРИПТОСИСТЕМ»
Навчальні питання
3.2.1 Методика криптоаналізу RSA
3.2.2 Характеристика методів криптоаналізу.
3.2.3 Двійкове решето
3.2.4 Сутність методу ρ-Поларда
Додаток А 1.13 Криптоаналіз RSA та дискретних логарифмiв методом ![]() -Поларда. Приклади
розв’язку задач та задачі для самостійного розв’язання
-Поларда. Приклади
розв’язку задач та задачі для самостійного розв’язання
Додаток Б 1.14 Криптоаналiз RSA методом квадратичного решета. Приклади розв’язку задач та задачі для самостійного розв’язання
Джерела що рекомендуються для самостійної робот
1. Горбенко І.Д. Основи теорії захисту інформації. Електронний конспект лекцій. Харків, ХНУРЕ, 2005 р.
2. Горбенко І.Д. „Криптографічний захист інформації”. Навч. посібник Харків, ХНУРЕ, 2004 р.
В. Задірака . Компьютерная криптологія. Підручник. К, 2002 ,504с.
Додаткова література
1. А. Менезис, П. Ван Аршот, С. Ватсон. Руководство по прикладной криптографии CRC Press, 1997, электронная копия, 662 с
2.Брюс Шнайер. Прикладная криптография. М., изд. Триумф. 2002 г., 797 с
3.2.1 Методика криптоаналізу RSA
Таємні параметри: ![]() .
.
Відкриті параметри: ![]() .
.
Функція Ейлера ![]() є таємною. Основною задачею є пошук таємного
ключа
є таємною. Основною задачею є пошук таємного
ключа ![]() .
.
Можливі методи пошуку:
1)
оскільки множина пар ![]() є
кінцевою, то існує можливість „грубої сили”
є
кінцевою, то існує можливість „грубої сили” ![]() ;
;
2)
![]() можливість знаходження секретного ключа
можливість знаходження секретного ключа ![]() ;
;
3)
![]() .
.
Задача факторизації є основною складності алгоритму. Сутність криптоаналізу зводиться до факторизації. Найбільш простим методом є метод спробного поділу.
![]()
Очевидно, найбільш ймовірними є числа:
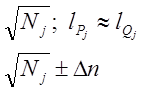 .
.
Візьмемо інтервал ![]() .
.
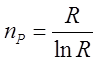 (3.2.6)
(3.2.6)
![]() –
максимальне просте число.
–
максимальне просте число.
В інтервалі ![]() існує
існує ![]() простих чисел:
простих чисел:
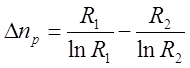 . (3.2.7)
. (3.2.7)
Кількість спроб підібрати число є колосальним і це не реалізуємо.
3.2.2 Характеристика методів криптоаналізу.
Історично відносно RSA були розроблені наступні методи:
- ρ-Поларда;
- р-1 Поларда;
- Ленстри на еліптичних кривих;
- двійкове решето;
- загальне решето числового поля;
- спеціальне решето числового поля.
ρ-Поларда метод – є метод створення колізій.
р-1 Поларда метод не знайшов застосування, є більш складний ніж ρ-Поларда метод.
Метод Ленстри – більш ефективний ρ-Поларда метода, але не достатній, йому не доступні числа більше.
Двійкове решето – найбільш ефективний метод, якщо довжина модуля ![]() біт.
біт.
Для більших довжин є загальні решета числового поля.
Для великих ![]() з великими простими множниками розкладання
на множники є серйозною проблемою, але не настільки, як потрібно. Разючою
ілюстрацією цього може служити наступна історія. У 1977 році три винахідники
алгоритму RSA наважилися запропонувати читачам популярного журналу Scientific
American розкрити шифроване повідомлення, яке вони розмістили в розділі «Математичні ігри» Мартіна Гарднера
(Martin Gardner). За розшифровку цього повідомлення вони запропонували нагороду
в 100 дол. За їхніми оцінками, задача не могла бути вирішена раніше, ніж
приблизно через 40 квадрильйонів років [10,18]. Але в квітні 1994 року група
користувачів Internet зажадала виплати призової суми після всього восьми
місяців спільної роботи в Internet. У запропонованій задачі використовувався
відкритий ключ довжиною в 129 десяткових знаків (довжина модуля N), що
дорівнює приблизно 428 бітам. З квітня 1996 р. до квітня 2003 р. були вирішені
задачі для RSA-130 [18], RSA-140, RSA-155, RSA-160. RSA-150 залишився
нефакторизованим та в подальшому відкликаний із переліку задач. Останньою з
вирішених задач є задача для RSA-576, у якій довжина ключа дорівнює 576 бітів.
За вирішення цієї задачі команда отримала 10000 дол. Задачі факторизації RSA
від RSA-640 до RSA-2048 залишаються відкритими, з нагородами відповідно від
20000 дол. до 200000 дол. Наявні на сьогодні результати наведено в табл. 1.1. Одиницею
вимірювання складності задачі в даному випадку є MIPS-рік – обсяг роботи,
виконуваної протягом року процесором, що здійснює обробку одного мільйона
команд у секунду, що приблизно еквівалентно виконанню 3*1013 команд.
Так, машина на базі Pentium з частотою 2000 МГц показує швидкість 500 MIPS.
з великими простими множниками розкладання
на множники є серйозною проблемою, але не настільки, як потрібно. Разючою
ілюстрацією цього може служити наступна історія. У 1977 році три винахідники
алгоритму RSA наважилися запропонувати читачам популярного журналу Scientific
American розкрити шифроване повідомлення, яке вони розмістили в розділі «Математичні ігри» Мартіна Гарднера
(Martin Gardner). За розшифровку цього повідомлення вони запропонували нагороду
в 100 дол. За їхніми оцінками, задача не могла бути вирішена раніше, ніж
приблизно через 40 квадрильйонів років [10,18]. Але в квітні 1994 року група
користувачів Internet зажадала виплати призової суми після всього восьми
місяців спільної роботи в Internet. У запропонованій задачі використовувався
відкритий ключ довжиною в 129 десяткових знаків (довжина модуля N), що
дорівнює приблизно 428 бітам. З квітня 1996 р. до квітня 2003 р. були вирішені
задачі для RSA-130 [18], RSA-140, RSA-155, RSA-160. RSA-150 залишився
нефакторизованим та в подальшому відкликаний із переліку задач. Останньою з
вирішених задач є задача для RSA-576, у якій довжина ключа дорівнює 576 бітів.
За вирішення цієї задачі команда отримала 10000 дол. Задачі факторизації RSA
від RSA-640 до RSA-2048 залишаються відкритими, з нагородами відповідно від
20000 дол. до 200000 дол. Наявні на сьогодні результати наведено в табл. 1.1. Одиницею
вимірювання складності задачі в даному випадку є MIPS-рік – обсяг роботи,
виконуваної протягом року процесором, що здійснює обробку одного мільйона
команд у секунду, що приблизно еквівалентно виконанню 3*1013 команд.
Так, машина на базі Pentium з частотою 2000 МГц показує швидкість 500 MIPS.
Таблиця 1.1 – Прогрес у розв’язку задач факторизації модуля N
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.