Между
максимальной степенью многочленов, для которых точна квадратурная формула, и
порядком точности квадратурной формулы, скажем, по отношению к шагу ![]() , с которым используются значения
подынтегральной функции, имеется прямая связь.
, с которым используются значения
подынтегральной функции, имеется прямая связь.
В связи с этим возникает
естественная задача о нахождении среди всех квадратурных формул с ![]() узлами, вида , квадратурной формулы с таким расположением узлов
узлами, вида , квадратурной формулы с таким расположением узлов ![]() на отрезке
на отрезке ![]() и с такими весами
и с такими весами ![]() ,
при которых она точна для алгебраических многочленов максимальной степени. Эта
степень меньше, чем
,
при которых она точна для алгебраических многочленов максимальной степени. Эта
степень меньше, чем ![]() , так как при любом выборе узлов
, так как при любом выборе узлов ![]() и весов
и весов ![]() ,
многочлен
,
многочлен ![]() степени
степени ![]() обладает
тем свойством, что
обладает
тем свойством, что  , но
, но 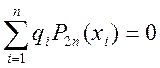 , то
есть приближенное равенство не может быть выполнено.
, то
есть приближенное равенство не может быть выполнено.
Рассмотрим стандартный отрезок ![]() . Пусть пока
. Пусть пока ![]() -
произвольные попарно непересекающиеся узлы. Тогда, если взять веса
-
произвольные попарно непересекающиеся узлы. Тогда, если взять веса
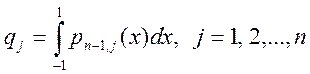
где
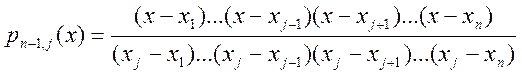
есть лагранжевы коэффициенты
для интерполяционного многочлена степени ![]() , то
квадратурная формула будет точна, во всяком случае, для многочленов степени
, то
квадратурная формула будет точна, во всяком случае, для многочленов степени ![]() .
.
Действительно, любой
алгебраический многочлен ![]() степени
степени ![]() точно восстанавливается интерполяционным
многочленом
точно восстанавливается интерполяционным
многочленом ![]() той же степени. Поэтому
той же степени. Поэтому
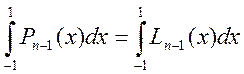 по определению многочлена Лагранжа
по определению многочлена Лагранжа 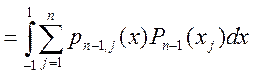
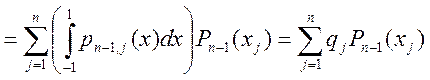 . А это и значит, что квадратурная формула
с такими параметрами точна для многочленов
. А это и значит, что квадратурная формула
с такими параметрами точна для многочленов ![]() степени.
степени.
Возьмем теперь в качестве узлов ![]() корни многочлена Лежандра
корни многочлена Лежандра ![]() , которые согласно Лемме расположены в
интервале
, которые согласно Лемме расположены в
интервале ![]() , а веса
, а веса ![]() найдем
по формуле .
найдем
по формуле .
Покажем, что квадратурная формула
с выбранными узлами и весами точна для многочленов степени ![]() и тем самым для многочленов максимальной
степени.
и тем самым для многочленов максимальной
степени.
Пусть ![]() -
произвольный алгебраический многочлен степени
-
произвольный алгебраический многочлен степени ![]() .
Представим его в виде
.
Представим его в виде ![]() , где
, где ![]() -
многочлены
-
многочлены ![]() степени (частное и остаток от деления
степени (частное и остаток от деления ![]() на многочлен
Лежандра
на многочлен
Лежандра ![]() )
)
В силу ортогональности многочлена
Лежандра ![]() к любому многочлену степени
к любому многочлену степени ![]() имеем
имеем
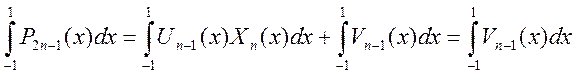
Поскольку ![]() - корни многочлена
Лежандра, то
- корни многочлена
Лежандра, то ![]() , тогда
, тогда
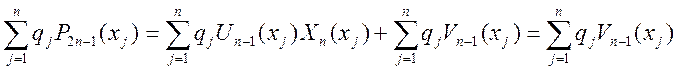
Поскольку квадратурная формула с заданными весами ![]() заведомо точна для многочленов степени
заведомо точна для многочленов степени ![]() , то
, то
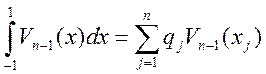 .
.
Отсюда и из равенств и приходим к доказываемому равенству
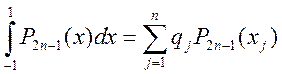 .
.
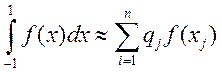
Квадратурная формула с ![]() указанными узлами и весами для многочленов
степени
указанными узлами и весами для многочленов
степени ![]() называется канонической квадратурной
формулой Гаусса.
называется канонической квадратурной
формулой Гаусса.
Можно доказать, что ее узлы ![]() расположены
симметрично относительной точки x=0, а веса
расположены
симметрично относительной точки x=0, а веса ![]() положительны и в
симметричных уздах совпадают при любом
положительны и в
симметричных уздах совпадают при любом ![]() . То
есть для формулы Гаусса-3 :
. То
есть для формулы Гаусса-3 : ![]() , для Гаусса-4:
, для Гаусса-4: ![]() . Численно узлы
. Численно узлы ![]() можно
рассчитать как корни j-го многочлена Лежандра , а веса
можно
рассчитать как корни j-го многочлена Лежандра , а веса ![]() по формуле .
по формуле .
Примечание: можно проверить, что при n=1 формула Гаусса совпадает с канонической формулой прямоугольников.
В силу построения, погрешность формулы Гаусса равна нулю для всех многочленов степени меньше 2n-1. То есть порядок точности Гаусса-2=3, Гаусса-3=5, а Гаусса 4=7.
Разобьем отрезок ![]() на N равных частичных отрезков
на N равных частичных отрезков ![]() , где
, где ![]() ,
, ![]() . На каждом частичном отрезке зададим N узлов:
. На каждом частичном отрезке зададим N узлов:
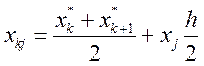 ,
, ![]()
где ![]() – узлы канонической формулы
Гаусса . Расположение узлов на частичном отрезке геометрически подобно расположению узлов канонической формулы. В силу этого, квадратурная формула:
– узлы канонической формулы
Гаусса . Расположение узлов на частичном отрезке геометрически подобно расположению узлов канонической формулы. В силу этого, квадратурная формула:
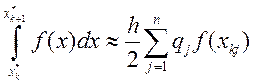 также точна для многочленов степени 2n-1.
также точна для многочленов степени 2n-1.
Суммируя соотношение по ![]() получаем усложненную квадратурную
формулу Гаусса:
получаем усложненную квадратурную
формулу Гаусса:
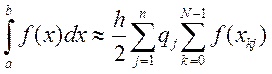
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.