Свойства:
1) Какое бы r>0, r<R: ряд 1 будет сходиться равномерно относительно х на [-r;r].
2) Сумма S(x) степенного ряда 1 для " х Î [-R;R] представляет непрерывную функцию. Доказательство из Т1 и свойства 1.
3) Если 2 степенных ряда в окрестности т. х=0 имеют одну и ту же сумму, то эти два ряда тождественны. Доказательство: положим х=0, затем диф. и положим х=0…
4) Если в точке х=R степенной ряд 1 расходится, то сходимость степенного ряда на промежутке (0;R) Не может быть равномерной. Доказательство: При равн. сходимости ряда 1 по Т3 можно в соотн. 1 перейти к lim почленно. Т.е. для этого ряд должен сходиться – противоречие.
5) Если степенной ряд 1 сходится при x=R хотя бы и не абсолютно, тогда $ равномерная сходимость соответствующего функционального ряда 1 на всем промежутке на [0;R]. Доказательство: через умножение, деление на Rn , а потом по Абелю.
6) Теорема Абеля. Если степенной ряд 1 сходится при х=R, то сумма ряда сохраняет непрерывность и при этом значении х.
7) Степенной ряд 1 в промежутке [0;x] |x|<R (х из промежутка сходимости) всегда можно проинтегрировать почленно.
8) Степенной ряд 1 внутри его промежутка сходимости можно дифференцировать почленно.(Т6)
9) Функция, представленная степенным рядом 1 на его промежутке сходимости имеет внутри этого промежутка производные всех порядков. Сам ряд – ряд Тейлора.
Теорема Коши-Адамара: Радиус сходимости ряда 1 есть величина обратная
наибольшему пределу ρ следующих величин:
.
Ряд Тейлора: f(x) [x0;x0+h], [x0-h;x0] h>0 имеет производные всех порядков, которые являются
непрерывными функциями. Тогда по свойству 9 она может быть представлена в виде(1)
. В таком виде – разложение Тейлора rn – остаточный член. Т.к. rn может быть сколь угодно большим, его можно заменить на
(2)«…». Такой ряд, независимо от того, сходится ли он или нет и имеет ли
своей суммой f(x), называется рядом Тейлора для функции f(x).
- коэффициенты
Тейлора. Т. к. разность между f(x) и суммой n + 1 члена
ряда Тейлора равна rn., то для
того, чтобы при некотором x имело место разложение (2), необходимо и достаточно,
чтобы дополнительный член rn->0 при этом x, при n->∞
. Т.е. при x=0 – ряд Маклорена.
Коэффициенты вычисляются по аналогичным формулам.
Остаточные члены в форме
Лагранжа: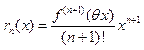 
В форме Коши: 
IV. Функциональные ряды.
Пусть
дана последовательность {fn(x)}, определенных на [a;b]. f(x),
определенную на [a;b] называют пределом функциональной последовательности fn(x), если для " x0Î[a;b] 
Рассмотрим ряд, составленный из fn(x). Сумма ряда S(x) =
. Частичная сумма
.
Равномерная сходимость: Функциональная последовательность fn(x) называется равномерно-сходящейся на x Î [a;b] в некоторой функции f(x), если для "ε >0 в последовательности функций $ fN(x), что для " n>N и "x Î [a;b]: |f(x)-fN(x)|<ε.
Свойства равномерно сходящихся последовательностей:
1)Если {fn(x)} и {gn(x)} сходятся к f(x) и g(x), λ и μ – константы, то {λfn(x)+μgn(x)} сходится к λf(x)+μg(x). 2)Если {fn(x)} равномерно сходится, а функция φ(x) ограничена на [a;b], то последовательность {fn(x)φ(x)} будет равномерно сходиться к f(x)φ(x) на этом промежутке.
Теорема о равномерной сходимости:
Для того, чтобы {fn(x)} равномерно сходилась на [a;b] к некоторой f(x) ó " ε>0 $N, который не зависит от х, что "n>N и "p,q>n выполнялось неравенство |fp(x)-fq(x)|<ε "xÎ[a;b] Доказательство: -> Пусть {fn(x)} -> x, выберем ε`>0. Тогда из определения: в последовательности $ fN(x) такая, что |fn(x)-f(x)|<ε`. Выберем две произвольные последовательности {fp(x)},{fq(x)}, p,q>N. И рассмотрим |fp(x)-fq(x)|=|fp(x)-fq(x)+f(x)-f(x)|≤ |fp(x)-f(x)|+|fq(x)-f(x)|≤ε`+ε`=2ε`. Выберем ε`=ε/2. ->доказана.
<- Пусть {fn(x)} удовлетворяет условию |fp(x)-fq(x)|<ε. Тогда она сходится для "х Î[a;b]. Это вытекает из теоремы Коши для последовательностей. Обозначим lim fn(x)=f(x) и пусть ε>0. В силу предположения в последовательности есть такая fN(x), что для "n>N выполняется |fp(x)-fq(x)|<ε. "p,q>n. "xÎ[a;b] или |fp(x)-fn(x)|<ε. Тогда lim(p->∞) |fp(x)-fn(x)|. Получим, что для "n>N: |f(x)-fn(x)|≤ε. Следовательно, fn(x) будет сходиться равномерно.
Теорема. lim{fn(x)} есть непрерывная функция.
Говорят,
что сходится равномерно "xÎ[a;b], если $ {Sn(x)} его
частичных сумм, которая сходится равномерно на [a;b]
Критерий
Коши: Для того, чтобы сходился равномерно на [a;b] ó для "ε>0 $ N, что для "n>N, " m>0 выполнялось: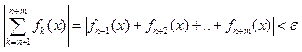
.
Признаки равномерной сходимости:
Вейерштрассе:
Пусть дан ряд (1) и сходящийся числовой ряд
. Если, начиная с некоторого N для "n>N: |fn(x)|≤an на
[a;b], то ряд 1 будет равномерно сходиться на [a;b]. Доказательство:
по сравнению с числовыми рядами и оценке |Sp(x)-Sq(x)|. p,q>N
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.