Функции многих переменных. Дифференцируемость и дифференциал функции в точке, страница 3

Лемма 1. Если F:U(x_0,y₀)->R, U(x₀,y₀) из R² и определена в этой окрестности и для нее выполнены следующие свойства: 1)Эта функция F p раз непрерывно дифференцируема. 2)В точке (x₀,y₀) F(x₀,y₀)=0 3) F_y’(x₀,y₀)!=0. Тогда $ такой промежуток I=I_xxI_y, Где I_x={x| |x-x₀|<α}; Iy={y| |y-y₀|<β }. Это множество I вложено в U(x₀,y₀). Кроме того, $ такая функция f Î C^p(I), что " (x;y) принадлежит U(x₀,y₀). При условии F(x₀,y₀)=0 |-> y=f(x). Причем производная y’ может быть вычислена(2) . Другими словами, уравнение F(x,y)=0 однозначно разрешимо относительно y и функция y=f(x) есть решение.

Лемма 2. Если F:U->R, где U из R^m+1. 1) F Î C^p(U;R). 2) F(x⁰,y⁰)=0 3)F`(x⁰,y⁰)!=0; Тогда $ (m+1)мерный промежуток I=I_x^mxI_y, где I_x^m – соответствующий параллелепипед в m-мерном пространстве.

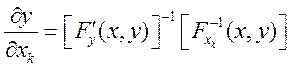
Теоремаонеявнойфункции: Если F: U->Rⁿ, Где U(x₀,y₀) из R^m+n 1)F Î C^(p) (U;Rⁿ), p≥1. 2)F(x₀,y₀)=0 3)|F`_y(x₀,y₀)|-обратимая матрица, т.е. определитель ее матрицы Якоби не равен 0. Тогда $ такой m+n мерный промежуток I=I_x^mxI_yⁿ, вложенный в U(x₀,y₀), I_x^m={x| |x_i –x_i⁰|<α_i i=1,m} I_y^m={y| |y_i –y_i⁰|<β_i i=1,n}. F(x,y)=0 ó f(x)=y. причем якобиан отображения f может быть представлен в виде: . . 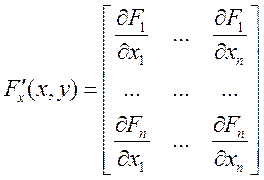Аналогично для y.

Диффеоморфизм: Отображение f:U->V (U,V – открытые подмножества пространства R^m) называется C^(p) диффеоморфизмом гладкости p (p=0,1,…), если: 1) f Î C^(p)(U;V). 2) f-биекция. 3) f^-1 Î C^(p) (V;U)

Теорема об обратной функции: Если f:G->Rm таково, что 1)f Î C^(p) (G,R^m); 2) y₀=f(x₀) x₀ Î G. 3) f’(x₀) – обратимая матрица. Тогда $ окрестность x₀ в области G : U(x₀) вложено в G и V(y₀) такие, что f:U(x₀)->V(y₀) есть C^(p) диффеоморфизм При этом " x Î U(x₀):y=f(x) имеет место соотношение (f^-1(y))’=(f’(x))^-1.

Приложение теоремы об обратной функции.  Полярные координаты. Отображение F:R²_t->R², R²_t ={(r,φ):r≥0}, которое можно определить следующим образом(1):x=rcos(φ), y=r sin(φ); якобиан этого отображения 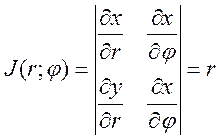. Якобиан этого отображения отличен от нуля, т.е. формулы(1) локально обратимы и значит, r и φ могут быть приняты в качестве новых координат точек плоскости, координаты которой раньше задавали х и у.

Сферическая система координат: z=rcos(φ);y=rsin(φ)sin(φ);x=rsin(φ)cos(φ); J=r²sin(φ)

Зависимость функций. Система функций f_i(x₁,x₂,…,x_m),i=1,n называется функционально-независимой в окрестности точки x₀, если для " непрерывной функции F(y₁,y₂,…y_n), определенной в окрестности точки y₀ =(f₁(x₀),f₂(x₀),…,(f_n(x₀)), соотношение F(f₁(x₀),…,f_n(x₀))=0 в окрестности точки x₀ тогда и только тогда, когда F(y₀)=0 в окрестности т y₀. Если для системы функций это условие не выполняется, то она называется функционально зависимой.

Лемма 1. Если система функций f_i(x₁,x₂,…,x_m),i=1,n гладких и определенных в окрестности U(x₀) такова, что матрица Якоби для " х Î U(x₀) имеет один и тот же ранг К, то 1) при к=n система функций функционально независима в окрестности. 2) при к<n найдется такая U(x₀) и такие к функций системы, что в окрестности x₀ n-k функций системы будут иметь представление: f_i(x)=g_i(f₁(x),…,f_k(x)),i=1,n

Лемма 2. Если f:G->Rm – это диффеоморфизм открытого множества G, то " х Î G найдется такая окрестность, в которой справедливо

Множество S вложенное в Rⁿ будем называть к-мерной гладкой поверхностью в Rⁿ, если " x₀ Î S существует U(x₀) вложенная в Rⁿ и диффеоморфизм φ:U(x₀)->Iⁿ, Iⁿ={t Î Rⁿ: |t_i|<1, i=1,n} вложено в Rⁿ, при котором S U(x₀) порождает образ этого пересечения, совпадающий на единичном кубе с частью к-мерной плоскости R^n.

Если к-мерная поверхность S, 1≤k≤n в U(x₀) задана параметрически с помощью гладкого отображения x(t): (t1,t2,…,tk)|->(x1,x2,…,xn) такого, что x₀=x(0) и матрица Якоби в точке 0 имеет ранг k, то k-мерная плоскость в Rn задаваемая равенством (1) x-x₀=x’(0)t называется касательной плоскостью или касательным пространством к поверхности S в точке x₀.

Условный экстремум – экстремум функции на заданной области.

Необходимый признак: Пусть f:D->R – функция определенная на открытом D из Rn и принадлежит C⁽¹⁾(D;R). Пусть S- Гладкая поверхность в области D. Для того, чтобы т.x0 Î S и не критичная для f была точкой локального экстремума функции f на поверхности S необходимо условие:

Достаточный признак: Пусть f:D_>R определена на открытом множестве D вложенном в Rn и f Î C⁽²⁾(D;R). S-гладкая поверхность области D, определенная 1. Функции Fi тоже принадлежат C⁽²⁾(D;R). Ранг системы F1,…,Fm в любой точке области D Равен m, т.е.  функционально независимы. Пусть дана Ф.Лагранжа.

L(x,λ)=f(x)-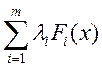и параметры λ1,…λm выбраны в соответствии с соотношением (необходимым признаком)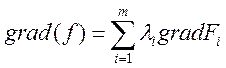(7) существования условного экстремума. Для того, чтобы критическая точка x₀ функции f На поверхности S была точкой экстремума достаточно, чтобы квадратичная форма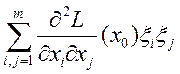 была знакоопределена для " векторов ξ из  . Если положительно определена, то x₀ –строгий локальный минимум, если отрицательно, то x₀ – строгий локальный максимум.