Системы дифференциальных уравнений. Системы линейных дифференциальных уравнений. Метод Коши, страница 4

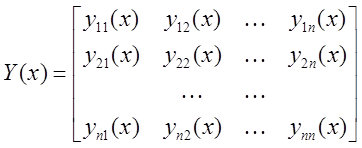 где                                                                                                                                                   (2)

 с начальными значениями: .                                                                                                                                             (3)

Теорема. Если матрица  непрерывна на , а определитель матрицы , то на  существует единственное решение уравнения (1) и определитель Вронского этого решения не обращается в ноль ни в одной точке .

Будем рассматривать одновременно с системой (1) систему вида:

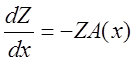                                                                                                                                                                                      (4)

Уравнение (4)  называется сопряженным для уравнения (1).

Теорема. Пусть  - решение (1), а матрица  непрерывна на , тогда  - существует на  и является решением системы (4).

Доказательство: По предположению теоремы решение  на  существует и определитель этого решения не равен нулю в любой точке , следовательно, существует обратная матрица  . А так как , то продифференцировав это соотношение, получаем:  ,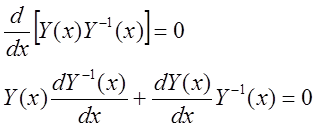

 где  - решение уравнения (1), следовательно, 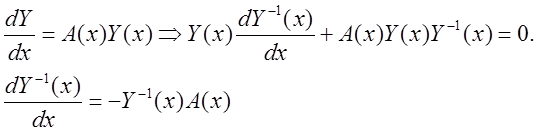 g

Рассмотрим систему - линейно независимых неоднородных  дифференциальных уравнений

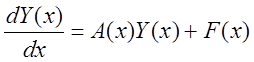 .                                                                                                                                                                      (5)

Будем искать решение этой системы методом вариации постоянной.

Обозначим - решение (1). Будем искать решение системы (5) в виде:

,                                                                                                                                                                               (6)

где - неизвестная вектор-функция.

Подставим (6) в (5):

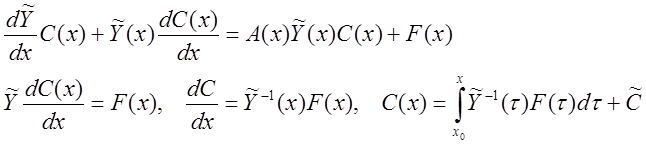
Тогда общее решение неоднородной системы будет иметь вид:

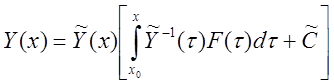                                                                                                                                                            (7)

Теорема. Общее решение неоднородной системы (5) можно представить в виде: 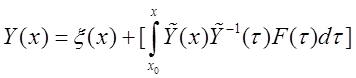,                                                                                                                       (8)

 где - общее решение соответствующей однородной системы.

Замечание. Пусть матрица постоянна и  начальные условия имеют вид: 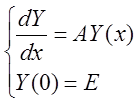                                                                                                                 (9)

Покажем, что решение уравнения (9) -  удовлетворяет функциональному уравнению:

.                                                                                                   (10)

 При любом фиксированном  матрицы  и  будут решением (9). При эти матрицы будут совпадать в силу начальных условий и, следовательно, по теореме о существовании и единственности они будут совпадать для любых . Если воспользоваться (10), то можно записать (сделав замену , и умножив соотношение (10) справа на ):

.                                                               (11)

Сравнив (11) и (7),  сделаем вывод о том, что общее решение неоднородной системы ДУ с постоянной матрицей А может быть представлено в виде:

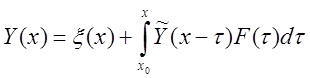.                                                                               (12)