Расчёт магнитных полей с помощью закона Био–Савара–Лапласа. Магнитное поле в веществе (Главы 3-4 учебного пособия по общей физике), страница 5

Работа по перемещению контура на конечное расстояние

,

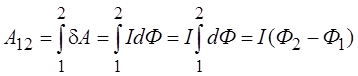где Ф₂ и Ф₁ – значения магнитного потока через контур в начальном и конечном положениях контура.

Необходимо отметить, что последний результат имеет общий характер, он не зависит от того, как именно изменялось положение контура в пространстве.

3.10.  Теорема Гаусса для магнитного поля

Теорема Гаусса для электростатического поля рассматривалась в разд. 1.6. Аналогичная теорема существует и для магнитного поля. Рассмотрим её.

В теореме Гаусса для магнитного поля рассматривается поток вектора магнитной индукции через замкнутую поверхность.

Найти величину магнитного потока можно следующим образом.

Силовые линии магнитного поля всегда замкнуты.

Поэтому, в отличие от силовых линий электростатического поля, они не могут начинаться или заканчиваться внутри замкнутой поверхности.

Другими словами, количество силовых линий магнитного поля, входящих в замкнутый объём, всегда равно количеству линий, выходящих из него.

Но это означает, что суммарный поток вектора магнитной индукции через замкнутую поверхность равен нулю

.

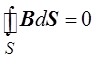Это и есть теорема Гаусса для магнитного поля.

Теорема Гаусса для электростатического поля показывает, что источником электрического поля являются заряды: .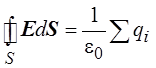

Теорема Гаусса для магнитного поля показывает, что магнитных зарядов в природе не существует (это уже отмечено в
разд. 3.5).

3.11.  Закон полного тока

Рассмотрим магнитное поле, созданное бесконечным прямым проводником с током I.

Как было установлено ранее, силовые линии такого тока – окружности с центром на проводнике, а индукция магнитного поля .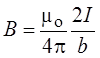

Вычислим для этого поля циркуляцию вектора магнитной индукции , т. е. интеграл от скалярного произведения вектора магнитной индукции на элемент контура dl, взятый по некоторому замкнутому контуру.

Для этого прежде всего необходимо выбрать контур.

В данном случае удобнее всего в качестве контура выбрать окружность, совпадающую с силовой линией магнитного поля.

Для такого контура Bdl = Bdl, так как в любой точке В параллелен dl и косинус угла между этими векторами равен единице. Поэтому

.

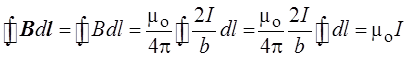Таким образом, циркуляция вектора В оказалась равна произведению магнитной постоянной на ток, охваченный контуром интегрирования:

.

Можно показать, что полученный результат не связан с формой контура интегрирования и имеет общий характер.

Если магнитное поле создано несколькими токами, то индукция магнитного поля в любой точке может быть найдена на основе принципа суперпозиции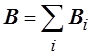, где В_i – индукция магнитного поля, созданного i-м проводником с током.

Циркуляция каждого из векторов В_i будет равна произведению силы i-го тока на магнитную постоянную .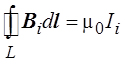

В свою очередь циркуляция вектора В по замкнутому контуру будет равна

,

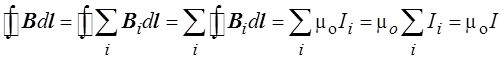т. е. циркуляция вектора магнитной индукции по контуру, охватывающему несколько токов, равна произведению m_о на алгебраическую сумму токов, охваченных этим контуром.

Полученное выражение для циркуляции вектора магнитной индукции имеет общий характер и называется законом полного тока*.

Знак тока в алгебраической сумме определяется простым правилом: ток, охватываемый контуром, положителен, если его направление совпадает с направлением положитель-ной нормали к контуру (см. рисунок).

Направление положительной нормали определяется правилом правого винта: если правый винт вращать по выбранному направлению обхода контура, то направление поступательного движения винта покажет направление положительной нормали n.

Закон полного тока удобно использовать для расчёта магнитных полей, созданных токами, которым свойственна симметрия (см. следующий раздел).

3.11.1.  Магнитное поле бесконечного соленоида

Соленоидом называется проводник, намотанный на цилиндрическую поверхность.

Если витки соленоида намотаны вплотную друг к другу, то соленоид удобно представлять в виде совокупности витков одинакового радиуса, расположенных параллельно друг другу вдоль оси соленоида. Центры витков расположены на оси, плоскости витков перпендикулярны оси. Токи во всех витках одинаковы.

Как показано в разд. 3.4, вектор магнитной индукции на оси витка параллелен ей. Следовательно, и суммарное поле всех витков на оси соленоида параллельно этой оси.