Линейные операторы. Поля. Следствия из аксиом поля. Поле комплексных чисел, страница 2

Самостоятельно доказать, что в случае выполнимости умножения оператора имеют место следующие свойства:

А(ВС) = (АВ)С;

 (ВА) = (В)А;

 (А+В)С = АС+ВС;

А(В+С) = АВ+АС;

Доказательство. Пусть В:ХY, С:ХY, A:YZ. Тогда

А(В+С)х = А((В+С)х) = А(Вх+Сх) = А(Вх)+А(Сх) = (АВ)х+(АС)х хХ.

А^n+m = Aⁿ+A^m, где Aⁿ = А^.А^.…^.А.

Определение. Оператор I w_XX называется тождественным (или единичным) оператором, если 

Ix = xхХ.

Определение. Линейный оператор В w_XX  называется обратным оператором к А (обозначают В = А^-1), если

АВ = ВА = I.

Любой линейный оператор А переводит нулевой вектор в нулевой вектор, т.е.

А(_X) = А(0х) = 0(Ах) = _Y.

Образ R(А) линейного оператора А w_XY  есть подпространство пространства Y. Действительно, пусть у₁, у₂R(А), т.е. у₁ = Ах₁, у₂ = Ах₂. Тогда

₁y₁+₂y₂  = ₁Ах₁+₂Ах₂ = А(₁х₁+₂х₂), т.е. ₁y₁+₂y₂R(A).

Определение. Размерность образа называется рангом оператора и обозначается rgA.

Определение. Множество всех хХ, удовлетворяющих равенству Ах = , называется ядром оператора А и обозначается N(A) или N_A.    

N(A) – подпространство пространства Х.

Действительно, пусть х₁,х₂N(A), т.е. Ах₁ =  и Ах₂ = . Тогда

А(₁х₁+₂х₂) = ₁Ах₁+₂Ах₂ = ₁+₂ = , т.е. ₁х₁+₂х₂N(A).

Определение. Размерность ядра называется дефектом оператора А и обозначается n_A.

Рассмотрим соотношение между рангом и дефектом линейного оператора.

Пусть А:ХY. Разложим Х в прямую сумму Х = N(A)  M_A, где M_A – любое дополнительное подпространство к N(A).

Выберем произвольный хХ и представим его в виде х = х_N +х_M, где х_NN(A), x_MM.

у = Ах = А(х_N+х_M) = Ах_N+Ах_M = +Ах_M = Ах_M.

Поэтому любой вектор из R(A) имеет хотя бы один прообраз из М_А. На самом деле этот прообраз единственный. Действительно, пусть для некоторого уR(A) имеем два прообраза и М_А. Тогда

 = у – у = А – А = А( – ), т.е. (–)N(A).

С другой стороны, т.к. М_А – подпространство, то (– ) М_А. Другими словами, ( – ) (N(A)М_А), которое состоит только из нулевого вектора (т.к. сумма прямая). Cледовательно, –=  и = _.

Т.о., мы установили взаимно однозначное соответствие (изоморфизм) между векторами подпространств R(A) и М_А, что позволяет записать:

dimX = n_A +dim М_А =  n_A +rgA.

Определение. Оператор А:ХXназывается взаимно однозначным, если двум различным элементам х₁,х₂  отвечают различные у₁ = Ах₁ и у₂ = Ах₂.

Если оператор А взаимно однозначный, то каждый уХ представляет собой образ некоторого хХ: у = Ах.

Для того, чтобы убедиться в этом, достаточно показать, что линейно независимые векторы е₁,е₂,…,е_n пространства Х отображаются оператором А в линейно независимые векторы Ае₁,Ае₂,…,Ае_nэтого же пространства. Рассмотрим

₁Ае₁+₂Ае₂+…+_nАе_n = А(₁е₁+₂е₂+…+_nе_n) = .

Т.к. оператор А – взаимно однозначный, то с учетом того, что А() = , получаем ₁е₁+₂е₂+…+_nе_n = , что возможно только при ₁ = ₂ = … = _n = 0 в силу линейной независимости е₁,е₂,…,е_n. Следовательно, система Ае₁,Ае₂,…,Ае_n – линейно независима.

у = ₁Ае₁+₂Ае₂+…+_nАе_n = А(₁е₁+₂е₂+…+_nе_n) = Ах.

Получается, что для взаимно однозначного оператора n_A = 0, а R(A) = Х.

Если q₁, q₂,…, q_m – линейно зависимая система векторов в Х, то система Аq₁,Аq₂,…, Аq_m также линейно зависимая.

Действительно, для линейно зависимой системы векторов в равенстве ₁q₁+₂q₂+…+_mq_m =  существуют _i0. Тогда

=А(₁q₁+₂q₂+…+_mq_m)=₁(Аq₁)+₂(Аq₂)+…+_m(Аq_m) при некоторых _i0,т.е. всякий линейный оператор сохраняет линейную зависимость системы векторов.

Пусть А:ХХ взаимно однозначный линейный оператор. Тогда определен обратный оператор А^-1:ХХ; если Ах = у, то А^-1у = х.

Покажем, что А^-1 – линейный оператор. Действительно,

А^-1(₁у₁+₂у₂) = А^-1(₁Ах₁+₂Ах₂) = А^-1А(₁х₁+₂х₂) = ₁х₁+₂х₂ =  =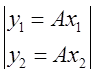

 = ₁А^-1у₁+₂А^-1у₂.

Определение. Линейный оператор А:ХХ называется невырожденным, если его ядро состоит только из нулевого вектора. В противном случае оператор называется вырожденным.

Взаимно однозначный оператор является невырожденным (n_A=0 или rgA=dimX=n). Верно и обратное.

Пусть А – невырожденный оператор. Докажем, что А – взаимно однозначный оператор. От противного. Пусть у = Ах₁ и у = Ах₂. Тогда  =у – у = Ах₁ – Ах₂ = А(х₁ – х₂). Отсюда х₁ – х₂ = (т.к. ядро состоит только из нулевого вектора) и х₁ = х₂.

Таким образом, невырожденный оператор является взаимно однозначным.

Произведение любого конечного числа невырожденных операторов будет также невырожденным оператором. Покажем это для двух операторов А и В (далее обобщение).

(АВ)х = А(Вх) =   ВхN(A)  Bx =   x =.

Сумма невырожденных операторов может быть уже вырожденным оператором. Например,