Курс общей физики для студентов ИДО. Часть II. Электростатика. Магнетизм. Колебания и волны: Учебное пособие, страница 4

Если поверхность замкнутая, поток вектора напряжённости равен

,    

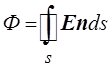т. е. интеграл берётся по замкнутой поверхности s.

В этом случае принято направлять вектор n наружу от поверхности. При этом поток через замкнутую поверхность положителен, если суммарный заряд, охваченный замкнутой поверхностью, положителен.

Размерность потока вектора напряжённости [Ф]=В.м=Н.м²/Кл.

1.6.  Теорема Гаусса

Теорема Гаусса – основная теорема электростатики. Она устанавливает связь между потоком вектора напряжённости через замкнутую поверхность и суммарным зарядом, охваченным этой поверхностью.

Рассмотрим эту теорему.

Пусть электрическое поле создано положительным точечным зарядом q.

Найдём поток вектора напряжённости электрического поля через замкнутую поверхность, охватывающую этот заряд.

В качестве поверхности выберем сферу радиуса r, центр которой совпадает с зарядом q.

Будем считать, что векторы n во всех точках замкнутой поверхности направлены от центра сферы.

Поскольку заряд, создающий поле, положителен и распо-ложен в центре сферы, постольку угол между вектором Е и вектором n во всех точках поверхности равен нулю.

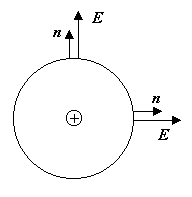Поэтому поток вектора напряжённости через элементарную поверхность ds будет равен Еnds = Ecosads = Ecos0ds = Eds.

Другими словами, в рассматриваемой ситуации скалярное произведение вектора напряжённости электростатического поля на вектор элементарной поверхности ра-вен произведению модулей этих век-торов.

Напряжённость поля, созданного то-чечным зарядом, равна .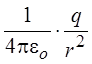

Поскольку заряд расположен в центре сферической по-верхности, расстояние от заряда до поверхности во всех её точках одинаково и равно r. Следовательно, модуль вектора напряжённости во всех точках сферической поверхности одинаков: E = const.

Константу можно вынести за знак интеграла, поэтому поток вектора напряжённости через замкнутую поверхность в данном случае равен .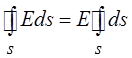

Интеграл от элементарных площадей поверхности s, взятый по всей поверхности, равен площади этой поверхности s.
В данном случае поверхность является сферой, площадь которой s = 4pr².

Таким образом, поток вектора напряжённости через замкнутую поверхность в данном случае равен .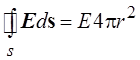

Подставив выражение для расчёта напряжённости, получаем

.

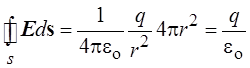Можно показать, что поток вектора напряжённости поля точечного заряда через замкнутую поверхность будет равен  и в том случае, когда заряд находится не в центре сферической поверхности.

Более того, поток будет таким же, даже если поверхность будет иметь любую форму.

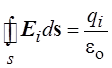Если поверхность охватывает несколько зарядов q_i, поток каждого из зарядов через замкнутую поверхность будет равен . Суммарный поток, созданный всеми зарядами, будет равен .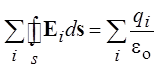

Меняя последовательность суммирования и интегрирования и учитывая, что в соответствии с принципом суперпозиции 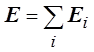, получаем 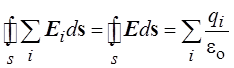, где Е – вектор напряжённости поля, созданного всеми зарядами, охваченными замкнутой поверхностью.

Итак, проведённый анализ позволил получить следующее соотношение:

.

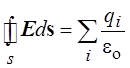Это соотношение имеет универсальный характер и называется теоремой Гаусса: поток вектора напряжённости электри-ческого поля через замкнутую поверхность равен отношению суммы зарядов, охваченных этой поверхностью, к электри-ческой постоянной.

Обратите внимание: в выражении теоремы Гаусса отсут-ствуют характеристики положения зарядов q_i.

Это означает, что поток вектора напряжённости не зависит от того, как расположены заряды, охваченные замкнутой поверх-ностью. Более того, поток вектора напряжённости не изменится, если изменится взаимное расположение зарядов, охваченных поверхностью.

Практическое значение теоремы Гаусса заключается в том, что с её помощью значительно упрощается расчёт полей, созданных симметричными распределениями зарядов. В этом случае можно выбрать поверхность такой формы, что 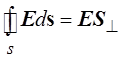, где S_^ – площадь части замкнутой поверхности, пронизываемой электрическим полем.

1.7.  Примеры расчёта напряжённости полей

с помощью теоремы Гаусса

Рассмотрим несколько примеров расчёта электростатических полей с помощью теоремы Гаусса.

1.7.1. Поле бесконечной равномерно заряженной

прямолинейной нити