Выберем
начало О прямоугольной системы координат в середине отрезка [FD],
представляющего собой перпендикуляр, опущенный из фокуса F на
директрису (предполагается, что фокус не принадлежит директрисе), а оси Ox и Oy направим
так, как показано на рис. 8.3. Пусть длина отрезка [FD] равна p.
Тогда в выбранной системе координат 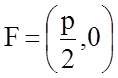 и каноническое уравнение параболы имеет вид
и каноническое уравнение параболы имеет вид
![]() .
(8.4.6)
.
(8.4.6)
Величина p называется параметром параболы.
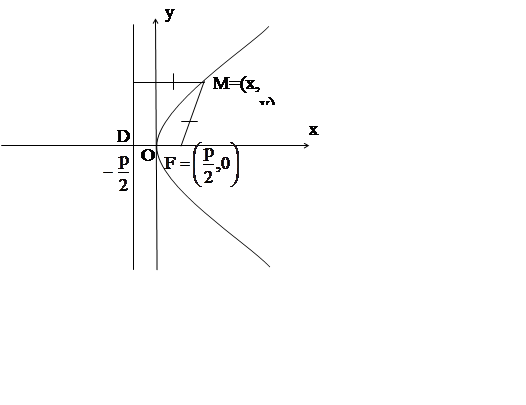 |
Парабола имеет ось симметрии, которая называется осью параболы. Точка пересечения параболы с ее осью называется вершиной параболы. Если парабола задана своим каноническим уравнением (8.4.6), то осью параболы является ось Ox. Очевидно, вершиной параболы является начало координат.
Пример 1. Точка А = (2,–1) принадлежит
эллипсу, точка F = (1,0) является его фокусом,
соответствующая F директриса задана уравнением ![]() . Составьте уравнение этого эллипса.
. Составьте уравнение этого эллипса.
Решение. Будем считать систему координат
прямоугольной. Тогда расстояние ![]() от
точки А до директрисы
от
точки А до директрисы ![]() в
соответствии с соотношением (8.1.8), в котором
в
соответствии с соотношением (8.1.8), в котором ![]() , равно
, равно
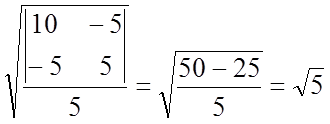 .
.
Расстояние ![]() от
точки А до фокуса F равно
от
точки А до фокуса F равно
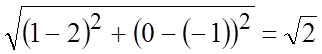 ,
,
что позволяет определить эксцентриситет эллипса
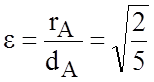 .
.
Пусть M = (x,y) – произвольная точка эллипса. Тогда расстояние ![]() от точки М до директрисы
от точки М до директрисы ![]() по формуле (8.1.8) равно
по формуле (8.1.8) равно
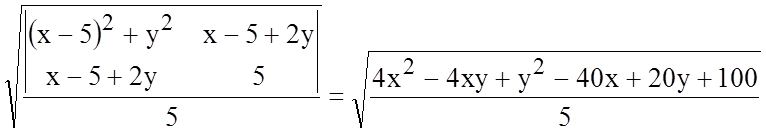 ,
,
а расстояние ![]() от
точки М до фокуса F равно
от
точки М до фокуса F равно
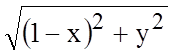 .
.
Поскольку для любой точки эллипса отношение 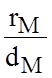 есть величина постоянная, равная
эксцентриситету эллипса, отсюда имеем
есть величина постоянная, равная
эксцентриситету эллипса, отсюда имеем
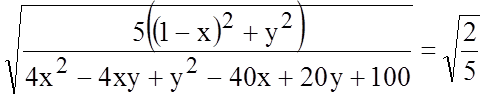
или
![]()
или
![]() .
.
Пример 2. Кривая задана уравнением
![]()
в прямоугольной системе координат. Найдите каноническую систему координат и каноническое уравнение этой кривой. Определите тип кривой.
Решение. Квадратичная форма ![]() имеет матрицу
имеет матрицу
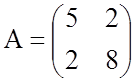 .
.
Ее характеристический многочлен
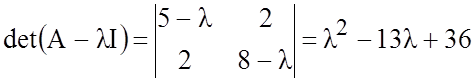
имеет корни l1 = 4 и l2 = 9. Следовательно, в ортонормированном базисе из собственных векторов матрицы А рассматриваемая квадратичная форма имеет канонический вид
![]() .
.
Перейдем к построению матрицы ортогонального
преобразования переменных, приводящего рассматриваемую квадратичную форму к указанному
каноническому виду. Для этого будем строить фундаментальные системы решений однородных
систем уравнений ![]() и ортонормировать их.
и ортонормировать их.
При ![]() эта
система имеет вид
эта
система имеет вид
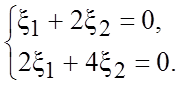
Ее общим решением является ![]() . Здесь одна свободная переменная. Поэтому
фундаментальная система решений состоит из одного вектора, например, из вектора
. Здесь одна свободная переменная. Поэтому
фундаментальная система решений состоит из одного вектора, например, из вектора
![]() . Нормируя его, получим вектор
. Нормируя его, получим вектор 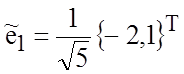 .
.
При ![]() также
построим вектор
также
построим вектор 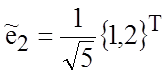 . Векторы
. Векторы ![]() и
и ![]() уже ортогональны, так как относятся к
различным собственным значениям симметричной матрицы А. Они составляют
канонический ортонормированный базис данной квадратичной формы. Из столбцов их
координат строится искомая ортогональная матрица (матрица поворота)
уже ортогональны, так как относятся к
различным собственным значениям симметричной матрицы А. Они составляют
канонический ортонормированный базис данной квадратичной формы. Из столбцов их
координат строится искомая ортогональная матрица (матрица поворота)
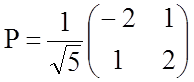 .
.
Проверим правильность нахождения матрицы Р по
формуле ![]() , где
, где ![]() – матрица квадратичной формы в базисе
– матрица квадратичной формы в базисе ![]() :
:
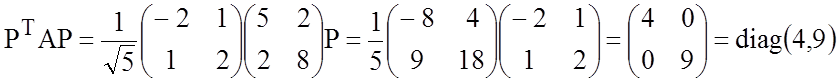 .
.
Матрица Р найдена верно.
Выполним преобразование переменных
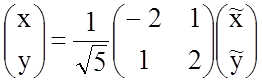
и запишем уравнение данной кривой в новой прямоугольной
системе координат со старым центром и направляющими векторами ![]() :
:
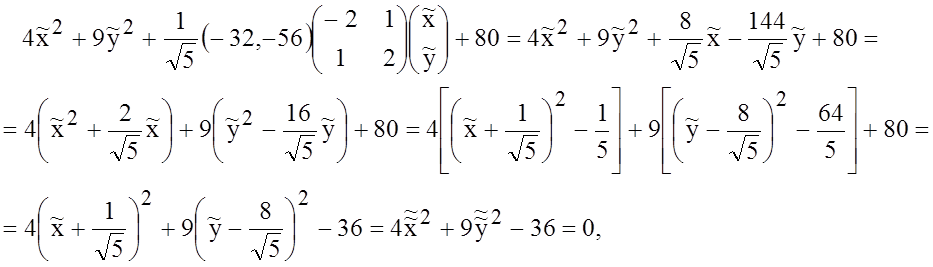
где 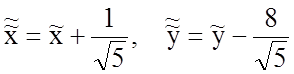 .
.
Получили каноническое уравнение эллипса
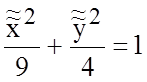 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.