





Дано: Диск (кольцо, цилиндр) к которому по касательной приложена сила F. Известна масса диска и радиус.
Требуется найти
1. Момент импульса, как функцию времени
2. Работу, как функцию времени
3. Угловую скорость, как функцию времени
Решение.
Рассмотрим общий случай, когда F=F(t)
1. Момент импульса
![]() , так как нас интересую только
проекции на ось z, то
, так как нас интересую только
проекции на ось z, то ![]() . Тогда,
т.к. для отдельно взятого тела I=const,
. Тогда,
т.к. для отдельно взятого тела I=const,
![]()
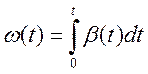 , (смотри пункт 3). Таким образом
, (смотри пункт 3). Таким образом
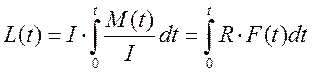 .
.
Примечание: В случае, когда F=const, ![]()
2. Работа.
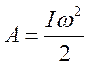 , соответственно,
, соответственно, 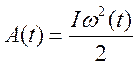 ,
, ![]() -
смотри пункт 3.
-
смотри пункт 3.
3. Скорость, как функция от времени.
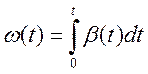 , причем
, причем 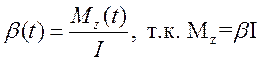 .
Но
.
Но ![]() т.к. сила приложена по касательной, то
т.к. сила приложена по касательной, то ![]() ,
,![]() . Таким образом
. Таким образом 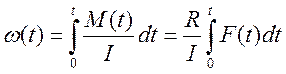 .
.
Примечание:
Момент инерции диска: 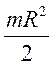 ,
цилиндра
,
цилиндра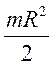 , кольца:
, кольца: ![]()
Дано: Заряженный шар, радиусом R,
зарядом +Q, вокруг него слой диэлектрика толщиной d, ![]() =2.
=2.
Найти: Потенциал в центре шара.
Решение
Потенциал связан с напряженностью электрического поля следующим соотношением:
![]() , или иначе
, или иначе 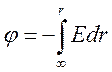 , полагая
, полагая ![]() .
.
Всю нашу среду, в которой нам нужно рассчитать разность потенциалов можно разделить на три части.
Рассмотрим каждую из этих частей по отдельности, а затем сложим.
Вне шара и вне диэлектрика.
Для того чтобы найти потенциал произвольной точки вне нашей системы, воспользуемся теоремой Гаусса для вектора смещения D.
![]() . В нашем случае
. В нашем случае
![]() . D
– константа,
. D
– константа, ![]() (по определению D).
В нашем случае
(по определению D).
В нашем случае ![]() =1, так
как берем точку в вакууме.
=1, так
как берем точку в вакууме.
Представим нашу вспомогательную поверхность, через которую
будем рассчитывать поток, как концентрическую сферу, радиусом ![]() . Тогда
. Тогда
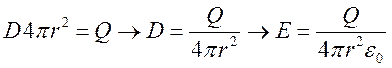
Тогда 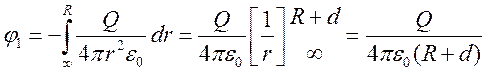
Внутри диэлектрика
Рассчитаем разность потенциалов на концах диэлектрика.
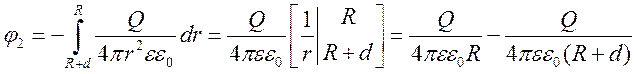
Внутри шара
Так как шар равномерно заряжен, плотность его заряда равна 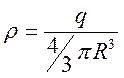 .
.
Отсюда, 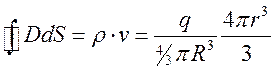 .
. 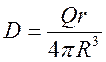 .
. 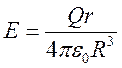
Тогда разность потенциалов:
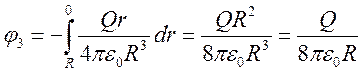
И суммарная разность потенциалов между центром шара и бесконечностью:
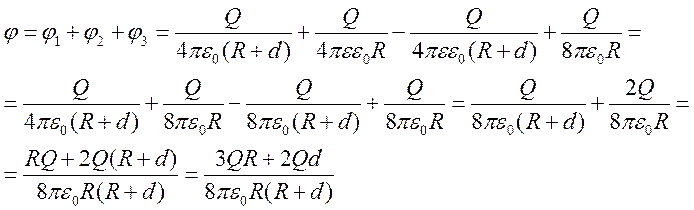
В магнитное поле влетают две частицы. Начинают двигаться
по окружности.
Первая по окружности радиуса r1, вторая по окружности радиуса r2. q1=q2. При
ускорении частицы прошли одинаковую разность потенциалов. Необходимо найти
отношение масс m1/m2.
Решение.
Так как частицы прошли одинаковую разность потенциалов, то
им сообщили одинаковую кинетическую энергию, а так как ![]() -
работа по перемещению заряда, и
-
работа по перемещению заряда, и ![]() ,
то
,
то ![]() .
.
На каждую из частиц действует сила Лоренца ![]() , а так как частицы движутся по окружности,
то
, а так как частицы движутся по окружности,
то ![]() . Кроме того, исходя из второго закона
Ньютона
. Кроме того, исходя из второго закона
Ньютона 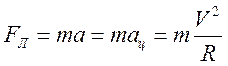 . Тогда
. Тогда
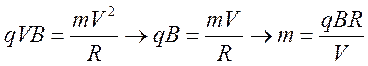
Найдем теперь соотношение масс. Однако учтем при этом, что частицы находятся в одном поле, поэтому B=const
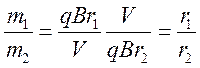
Заряженная частица движется в магнитном поле по окружности радиуса R , дано B и сказано, что данная частица под действием потенциальной силы U была предварительно Ускорена. Найти скорости частицы.
Решение.
Скорости частицы могут быть только ![]() -
угловая и линейная.
-
угловая и линейная.
На частицу в магнитном поле действует сила Лоренца:
![]() (в скалярном виде). Кроме того,
исходя из второго закона Ньютона
(в скалярном виде). Кроме того,
исходя из второго закона Ньютона 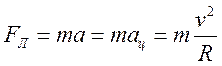 . Тогда
. Тогда 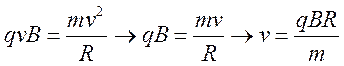
Так как частица обладает скоростью, то она обладает и кинетической энергией:
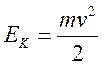 . Эту кинетическую энергию она
приобретает при разгоне в поле потенциальной силы U,
совершающей работу над частицей равную
. Эту кинетическую энергию она
приобретает при разгоне в поле потенциальной силы U,
совершающей работу над частицей равную ![]() .
Тогда:
.
Тогда:
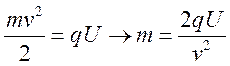 .
.
Подставляя это в формулу для линейной скорости получаем:
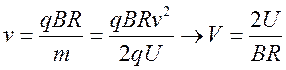 , а угловая скорость
соответственно:
, а угловая скорость
соответственно: 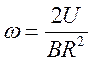
Ион влетает в магнитное поле и начинает двигаться по окружности, известно B. Найти кинетическую энергию иона, если известно, что магнитный момент электрического кругового тока равен p.
Решение.
По определению, кинетическая энергия 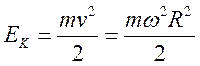 .
.
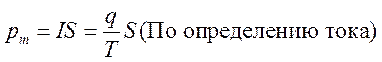 .
.
Период обращения 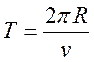 .
.
Рассматривая силу Лоренца по определению и с точки зрения
второго закона Ньютона, получаем (см. задачи выше): 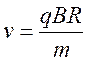
Тогда 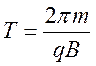 . Площадь поверхности,
ограниченной радиусом вращения
. Площадь поверхности,
ограниченной радиусом вращения ![]()
Тогда 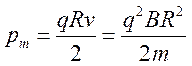
Выведем формулу угловой скорости через имеющуюся у нас формулу периода:
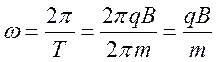
Подставим ее в формулу кинетической энергии:
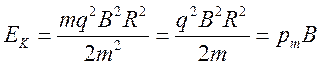
Частица массой m, зарядом q влетает в однородное магнитное поле перпендикулярно линиям напряженности, дан вектор B, скорость V. Найти магнитный момент.
Решение.
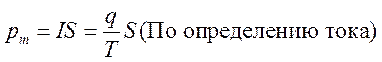 .
.
Период обращения 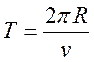 .
.
Рассматривая силу Лоренца по определению и с точки зрения
второго закона Ньютона, получаем (см. задачи выше): 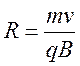
Тогда 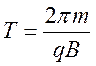 . Площадь поверхности,
ограниченной радиусом вращения
. Площадь поверхности,
ограниченной радиусом вращения ![]()
Тогда 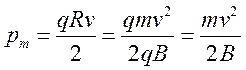
В магнитном поле заряд q массой m движется со скоростью V, причем B перпендикулярно силовым линиям. Определить момент сил.
Решение.
На частицу, движущуюся в магнитном поле, действует сила Лоренца.
Рассматривая силу Лоренца по определению и с точки зрения
второго закона Ньютона, получаем (см. задачи выше): 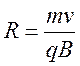
Соответственно при вращательном движении:
![]() , так как сила прикладывается по
касательной.
, так как сила прикладывается по
касательной.
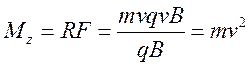
Дано:
Рамка с током в виде
квадрата/равностороннего треугольника со стороной ![]() , по ней течет ток
, по ней течет ток ![]() .
.
Найти:
Магнитную индукцию в центре симметрии. Точнее его модуль.
Решение:
Для начала определим куда
направлен вектор магнитной индукции в середине фигуры. По правилу буравчика
(большой палец потоку, остальные указывают направление магнитной индукции)
определяем, что все токи направлены в одном и том же направлении. Для
однозначности будем считать, ч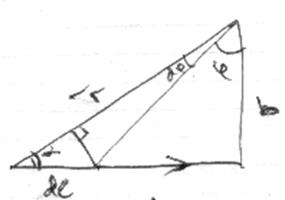 то ток у нас по рамке течет
против часовой стрелки, тогда вектор магнитной индукции будет направлен на нас,
в противном случае – от нас. Т.к. все три вектора направлены в одну и ту же
сторону, то суммарный вектор будет равен сумме всех векторов (у каждой стороны
свой вектор). Тогда
то ток у нас по рамке течет
против часовой стрелки, тогда вектор магнитной индукции будет направлен на нас,
в противном случае – от нас. Т.к. все три вектора направлены в одну и ту же
сторону, то суммарный вектор будет равен сумме всех векторов (у каждой стороны
свой вектор). Тогда ![]() , где
, где ![]() - количество сторон в правильной
фигуре (3 и 4 для треугольника и квадрата соответственно). Замечу, что
равенство магнитных индукций следует из того, что длины всех сторон равны,
токи, текущие по всем сторонам, тоже равны и расстояния до точки, в которой
следует посчитать магнитную индукцию также равны. Если это не так, следует
считать магнитную индукцию для каждой стороны отдельно.
- количество сторон в правильной
фигуре (3 и 4 для треугольника и квадрата соответственно). Замечу, что
равенство магнитных индукций следует из того, что длины всех сторон равны,
токи, текущие по всем сторонам, тоже равны и расстояния до точки, в которой
следует посчитать магнитную индукцию также равны. Если это не так, следует
считать магнитную индукцию для каждой стороны отдельно.
Теперь осталось применить формулу
БСЛ: 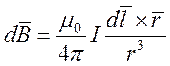 . Освободимся от
векторов:
. Освободимся от
векторов: 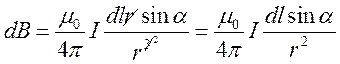 . Т.к. и
. Т.к. и ![]() , и
, и ![]() зависят от
величины
зависят от
величины ![]() , попробуем от
них избавиться:
, попробуем от
них избавиться: 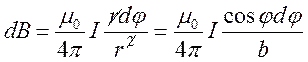 . Теперь
вспомним, какая фигура нам дана:
. Теперь
вспомним, какая фигура нам дана:
1) для треугольника
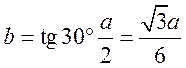 . Подставляем в полученное
выражение, мы получаем:
. Подставляем в полученное
выражение, мы получаем: 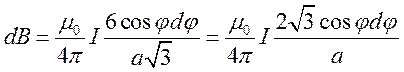 .
Теперь исполь
.
Теперь исполь зуем формулу
зуем формулу ![]() .
Т.к. угол
.
Т.к. угол ![]() изменяется
в пределах
изменяется
в пределах 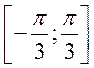 , получаем
конечный интеграл:
, получаем
конечный интеграл: 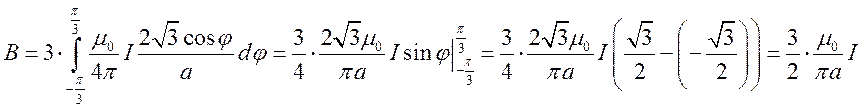 .
.
2) для квадрат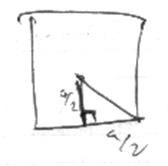 а
а 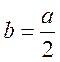 .
. 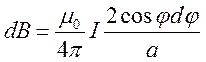 .
. 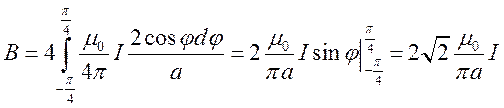 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.