Индивидуальная работа № 1 по дисциплине "Функциональный анализ" (Доказать сходимость и эквивалентность норм. Расстояние от элемента до подпространства многочленов нулевой степени)

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Индивидуальная работа №1

По дисциплине: Функциональный анализ

Группа: ПМ-22

Выполнил:

Савлюк В.И.

Проверила:

Иткина Н.Б.

г. Новосибирск

2004
1. Пусть Х – линейное пространство k раз дифференцируемых функций на [a;b]. Будет ли нормой

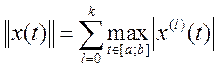
Решение.

Проверим, выполняются ли аксиомы нормы.

1.

            Так как , то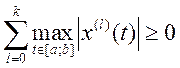

            Если x=0, то очевидно, что сумма обращается в ноль, так как каждый ее член становится равным нулю. Обратно, если сумма равна нулю, то ее члены либо все равны нулю, либо разных знаков, но так как мы определенно знаем, что каждый элемент суммы , то это становится возможным, когда все элементы суммы равны нулю. Значит , то есть элемент пространства – нулевой элемент.

2.  

   

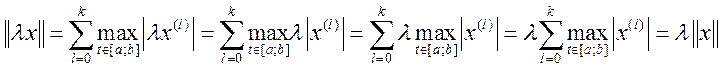
3.

           

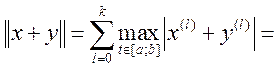
Но т.к.

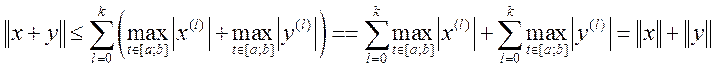
Все аксиомы нормы выполнены, значит 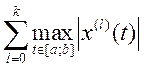 является нормой в заданном пространстве.

2. Доказать сходимость

            к , если 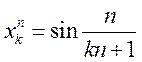 , , 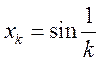в пространстве сходящихся к нулю последовательностей с нормой .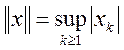

Решение.

            Если, последовательность сходится к, должно выполняться следующее свойство:

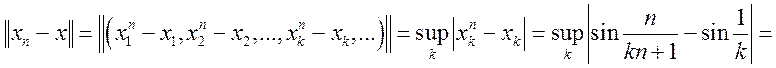
Рассмотрим модуль разности

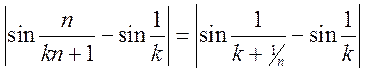. Каждый член разности являет собой функцию от аргумента, который лежит в пределах (т.к. ). На этом промежутке функция синуса является строго возрастающей, а значит, большему аргументу соответствует большее значение функции. Тогда мы можем избавиться от модуля следующим образом:

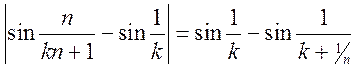
Причем очевидно, что

.

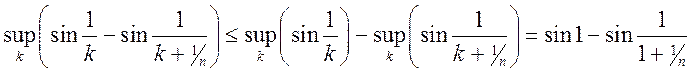Выведем зависимость , используя то, что функция синуса непрерывна и возрастает на [0;1]

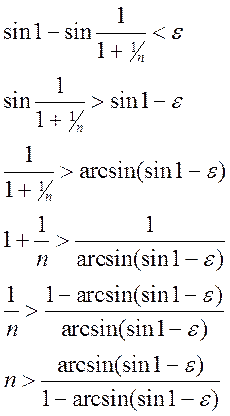
Таким образом, мы доказали сходимость, исходя из определения.

3. Доказать эквивалентность норм:  и

Нормы называются эквивалентными, если , где .

Норма в :

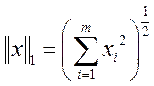
Норма в :

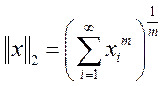
Доказательство:

1.

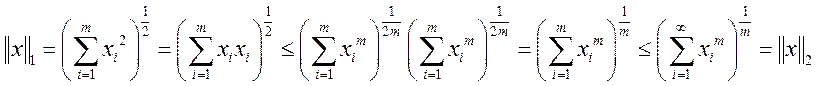
2.

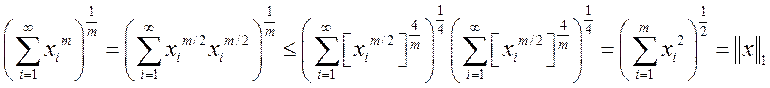
Все условия выполнены, что и требовалось доказать

4. В пространстве  найти расстояние от элемента  до подпространства многочленов нулевой степени.

По определению расстояния от элемента пространства до элемента подпространства L.

В пространстве  стандартная норма вводится следующим образом:

С учетом того, что множество многочленов нулевой степени , запишем

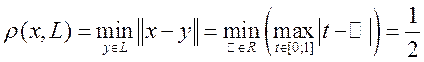
Ответ: