Евклидово пространство. Простейшие свойства евклидова пространства. Свойства ортонормированного базиса, страница 2

Определение Углом между векторами х,уЕ назовем угол, косинус которого определяется выражением

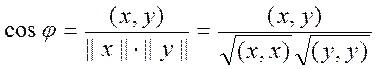, где .

Это определение корректно, Т.к. в силу неравенства Коши – Буняковского дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.

Определение. Два ненулевых вектора х и у называются ортогональными, если угол  между ними равен , т.е. если (х,у)=0.

Теорема Пифагора. Если х, уЕ ортогональны, то ||х+у||²=||х||²+||у||², т.е. квадрат гипотенузы равен сумме квадратов катетов.

Доказательство:

 ||х+у||²=(х+у,х+у)=(х,х)+ (х,у)+(у,х)+(у,у)=||х||²+||у||².

Обобщение теоремы Пифагора. Если x, y,…,z – ортогональные векторы, то

||х+у+…+z||²=||х||²+||у||²+…+||z||².

В евклидовом пространстве особую роль играют ортонормированные базисы.

Ортонормированный базис конечномерного евклидова пространства.

Определение. Будем говорить, что n векторов е₁, е₂,…, е_n  n-мерного евклидова пространства Е образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих векторов равна единице, т.е. если

(e_i,e_k) =

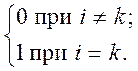
Если же (e_i,e_k)=0 при ik и (e_i,e_i)1, то базис называется ортогональным. Установим корректность приведённого определения, т.е. докажем, что векторы е₁, е₂,…, е_n  линейно независимы. Для этого покажем, что равенство  возможно лишь, когда . Действительно,

,

т.е.  Следовательно, векторы е₁, е₂,…, е_n линейно независимы и определение корректно.

Теорема 3. Во всяком n-мерном евклидовом пространстве Е существует ортонормированный базис.

Доказательство. Выберем базис f₁,f₂,…,f_n в Е. Построим ортонормированный базис е₁, е₂,…, е_n , векторы которого линейно выражаются через f₁,f₂,…,f_n. Начнем с построения ортогонального базиса g₁,g₂,…,g_n.

Положим

g₁= f₁,

g₂= f₂ +g₁.

g₂, т.к. f₂ и g₂ линейно независимы. Коэффициент  выберем из условия ортогональности g₂ и g₁: (g₂,g₁)=0.

(g₂,g₁)=( f₂+g₁, g₁)=(f₂,g₁)+ (g₁,g₁)=0.

Отсюда

=.

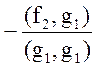Далее строим

g₃= f₃+g₁₊g₂.

g₃, т.к. f₃ ,g₁ и g₂ линейно независимы. Коэффициенты , выберем из условия ортогональности g₃ к g₁ и g₂: (g₃,g₁)=0 и (g₃,g₂)=0.

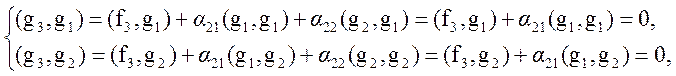
Откуда

, .

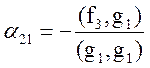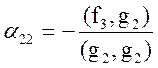Продолжая этот процесс, построим g₄,…,g_n-1. Останется выбрать g_n. Положим

g_n=f_n+g₁+g₂+…+g_n-1.

g_n 0, т.к. f_n, g₁,…,g_n-1 линейно независимы.

Потребуем, чтобы вектор g_n был ортогонален ко всем ранее построенным векторам, т.е.

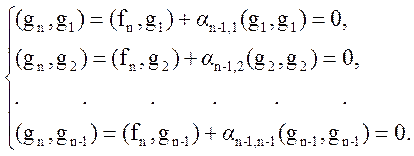
Отсюда находим:

 …,

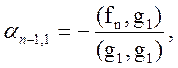
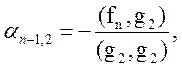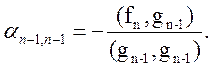
Ортогональный базис g₁,g₂,…,g_n построен.

Если теперь пронормировать каждый вектор, т.е.

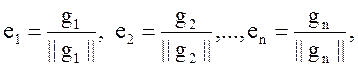
то получим ортонормированный базис е₁,е₂,…, е_n.

Процесс, использованный при доказательстве теоремы 3, называется процессом ортогонализации Грама – Шмидта.

Заметим, что в каждом n-мерном евклидовом пространстве Е существует много ортонормированных базисов.

Примером ортогонального базиса евклидова пространства Еⁿ всех упорядоченных совокупностей n вещественных чисел может служить следующий базис

е₁=(1,0,0,…,0), е₂=(0,1,0,…,0),…,  е_n=(0,0,0,…,1)

В этом случае

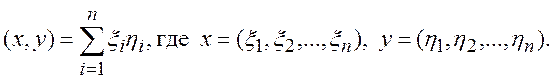
Свойства ортонормированного базиса

Пусть е₁,е₂,…, е_n – произвольный ортонормированный базис n-мерного евклидова пространства Е, а х и у – два произвольных вектора этого пространства. Найдем выражение скалярного произведения (х,у) через координаты векторов х и у в базисе е₁,е₂,…, е_n.

Пусть

,

.

Тогда

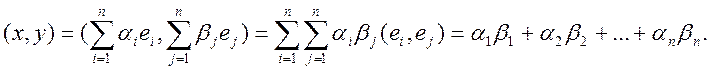
В ортонормированном базисе скалярное произведение двух любых элементов равно сумме произведений соответствующих координат этих элементов.

Если же базис f₁,f₂,…,f₃ не ортонормированный, то

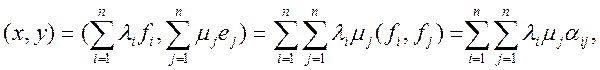
где , i=1,2,…,n;  j=1,2,…,n.

Таким образом, для того чтобы в данном базисе евклидова пространства скалярное произведение двух любых векторов было равно сумме произведений соответствующих координат этих векторов, необходимо и достаточно, чтобы базис был ортонормированным.

В общем случае

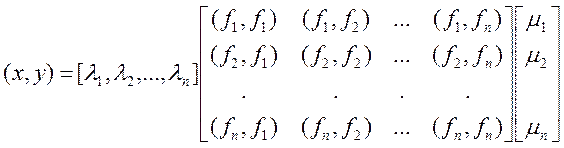
                               Матрица грамма (играет роль А)

Если  (f_i,f_j)=0, то матрица Грама диагональна.

Если

(f_i,f_j)=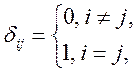

матрица Грама единична.

Вернемся к рассмотрению произвольного ортонормированного базиса е₁,е₂,…, е_n n-мерного евклидова пространства Е и выясним смысл координат произвольного вектора х относительно указанного базиса. Пусть

.

Тогда

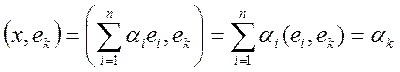, k=1,2,…,n.

Координаты произвольного вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на соответствующие базисные векторы. Эти скалярные произведения можно назвать (по аналогии с декартовыми координатами) проекциями вектора х на соответствующие базисные векторы.

Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения.

Определение Два множества F и G векторов евклидова пространства Е называются ортогональными, если каждый вектор из F ортогонален к каждому вектору из G. Ортогональность F и G обозначается так: FG.

Лемма 1. Для того чтобы вектор х был ортогонален к подпространству L, необходимо и достаточно, чтобы он был ортогонален ко всем векторам какого-либо базиса подпространства L.