где ![]() –
неизвестные функции;
–
неизвестные функции; ![]() – частные решения однородного
ДУ, соответствующего уравнению (8). Функции
– частные решения однородного
ДУ, соответствующего уравнению (8). Функции ![]() должны
удовлетворять уравнению (8). Но так как всего неизвестных функций n, то дополнительные (n – 1) условия, которым будут удовлетворять функции
должны
удовлетворять уравнению (8). Но так как всего неизвестных функций n, то дополнительные (n – 1) условия, которым будут удовлетворять функции ![]() можно выбрать произвольно [3]. Выберем эти
дополнительные условия следующим образом: производные функции
можно выбрать произвольно [3]. Выберем эти
дополнительные условия следующим образом: производные функции ![]() должны иметь такой же вид, какой они имели
бы при постоянных
должны иметь такой же вид, какой они имели
бы при постоянных ![]() . Например,
. Например, 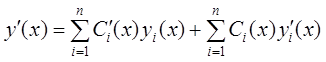 , но при постоянных
, но при постоянных ![]() –
–
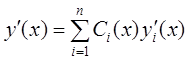 и, значит,
и, значит, 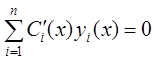 . Аналогично
получаем остальные ограничения:
. Аналогично
получаем остальные ограничения:
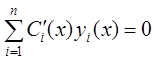 ,
,
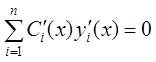 ,
,
..... ......
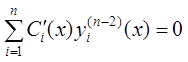 ,
,
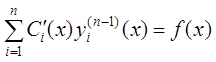 .
.
Решив эту систему, мы определим функции ![]() .
.
I. Определить тип дифференциальных уравнений и решить:
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. 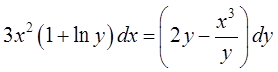 .
.
5. ![]() .
.
6. 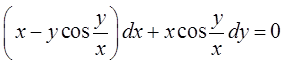 .
.
7. 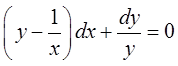 .
.
8. 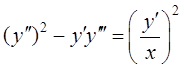 .
.
9. ![]() .
.
10. ![]() .
.
11. ![]() .
.
12. ![]() .
.
13. ![]() .
.
14. ![]() .
.
15. ![]() .
.
16. ![]() .
.
17. ![]() .
.
18. ![]() .
.
19. ![]() .
.
20. ![]() .
.
21. ![]() .
.
22. ![]() .
.
23. 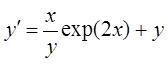 .
.
24. ![]() .
.
25. 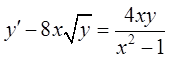 .
.
26. ![]() .
.
27. ![]() .
.
28. ![]() .
.
29. ![]() .
.
30. 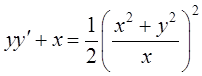 .
.
31. ![]() .
.
32. ![]() .
.
33. ![]() .
.
34. ![]() .
.
35. ![]() .
.
36. ![]() .
.
37. ![]() .
.
38. ![]() .
.
39. ![]() .
.
40. 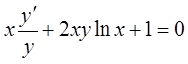 .
.
41. ![]() .
.
42. ![]() .
.
43. ![]() .
.
44. ![]() .
.
45. ![]() .
.
46. ![]() .
.
47. ![]() .
.
48. ![]() .
.
49. ![]() .
.
50. ![]() .
.
51. ![]() .
.
52. ![]() .
.
53. ![]() .
.
54. ![]() .
.
55. ![]() .
.
56. 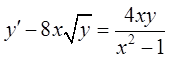 .
.
57. ![]() .
.
58. ![]() .
.
59. ![]() .
.
60. ![]() .
.
61. ![]() .
.
62. ![]() .
.
63. ![]() .
.
64. ![]() .
.
65. ![]() .
.
66. ![]() .
.
67. ![]() .
.
68. 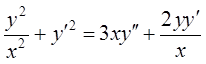 .
.
69. ![]() .
.
70. 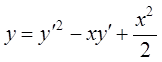 .
.
71. Определить область задания уравнения, область существования решения задачи Коши, область существования и единственности решения задачи Коши, особые решения.
1) 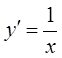 ;
2)
;
2) ![]() ; 3)
; 3) 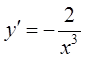 ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) 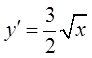 ;
7)
;
7) ![]() ; 8)
; 8) 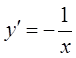 ;
9)
;
9) 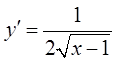 ; 10)
; 10) 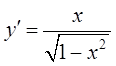 ;
11)
;
11) ![]() ; 12)
; 12) ![]() ; 13)
; 13) ![]() ;
14)
;
14) ![]() .
.
|
Номер варианта |
1 |
2 |
3 |
4 |
5 |
6 |
|
Номера задач |
1,2,3,4,64, 71(5) |
5,6,7,8,44,71(1) |
9,10,11,12, 69, 71(2) |
13,14,15,16, 66, 71(3) |
17,18,19,20, 65, 71(4) |
21,22,23,24, 67, 71(1) |
|
Номер варианта |
7 |
8 |
9 |
10 |
11 |
12 |
|
Номера задач |
25,27,30,36,64, 71(6) |
26,29,31,33,63, 71(7) |
32,34,47,38, 62, 71(8) |
35,39,40,41,61, 71(9) |
42,43,45,28,60,71(10) |
44,47,48,49,59,71(11) |
|
Номер варианта |
13 |
14 |
15 |
16 |
17 |
18 |
|
Номера задач |
50,1,4,51, |
2,5,8,10, |
3,7,8,12, |
13,18,20,44, 53,71(14) |
14,16,47, |
57,19,29, |
|
Номер варианта |
19 |
20 |
21 |
22 |
23 |
24 |
|
Номера задач |
21,28,36,48,63,71(2) |
22,25,39, |
24,26,33, |
28,35,38,43,64,71(9) |
29,31,56,41,59,71(11) |
17,19,44,46,61,71(12) |
|
Номер варианта |
25 |
|||||
|
Номера задач |
16,13,64,45, 70, 71(4) |
II. Решить систему линейных
неоднородных дифференциальных уравнений вида 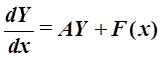 :
:
1) методом вариации постоянных
|
Номер варианта |
Матрица A, вектор правой части F |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
Продолжение таблицы
|
Номер варианта |
Матрица A, вектор правой части F |
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.