Дифференциальные уравнения n-ого порядка. Простейшие случаи понижения порядка

                Дифференциальные уравнения n-ого порядка.

                                                                    (1)

                                                                 (2)

Если уравнение разрешимо относительно старшей производной то  имеет вид (1). Так же уравнение n-го порядка можно представить в виде системы из n уравнений первого порядка.

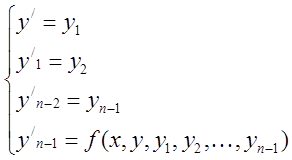                                                              (3)

Для уравнения n-ого порядка выполнены условия теоремы о существовании и единственности для системы так как (1)~(2)~(3).

               Простейшие случаи понижения порядка.

1.  Уравнение не содержат искомой функции и ее производной до порядка  k-1 включительно, то есть

.                 (4)

      В этом случае порядок может быть понижен до  заменой . Если из этого уравнения выразить  тогда решение y можно определить k-кратным интегрируемым функции p.

Пример.     .

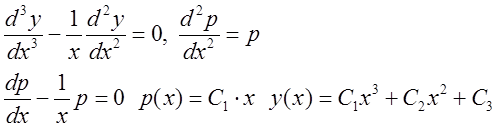2.  Уравнение, не содержащие неизвестного переменного

                                                                            (5)

В этом случае порядок можно понизить на единицу подстановкой .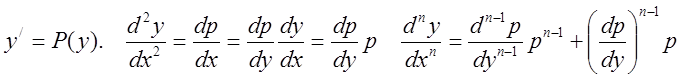

Пример. .

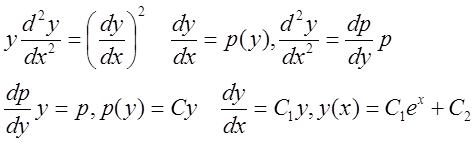3.  Левая часть уравнения

                                                                             (6)

есть производная некоторого дифференциального выражения (n-1)-го порядка. 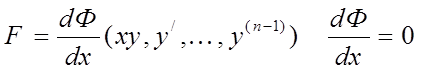. Если - решение последнего уравнения, следовательно, существует . Мы получили первый интеграл уравнения (6) и понизили на единицу степень решаемого уравнения.

Замечание. Иногда левая часть (6) становится производной дифференциального уравнения (n-1)-го порядка только при умножении на  поэтому здесь могут появиться лишнее решения (обращающие  в ноль) или мы можем потерять решение, если  разрывная функция.

Пример.

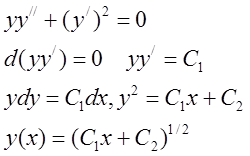
4.  Уравнение

                                                                                    (7)

однородно относительно  и его производных.

.

Или , где показатель определяется из условий однородности.

Порядок этого уравнения может быть понижен на единицу заменой: .

Если подставить эти соотношения в (7) и учесть однородность функции F, то в итоге в получим: .

Пример. .

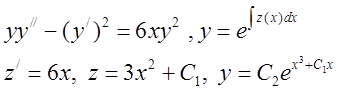                      Дифференциальные уравнения второго порядка,

                              допускающие понижение порядка.

1.  Пусть дано уравнение  .                                                (8)

                   Подстановка .

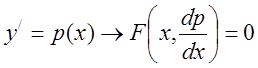 Если уравнение (8) можно разрешить относительно старшей производной, то уравнение   два раза интегрируется  по переменной  x.

Можно ввести параметр и заменить уравнение (8) его параметрическим представлением: 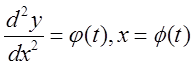. Воспользовавшись соотношением для дифференциалов:  , получаем:  и

II .                                                                                                                                                               (9)

Воспользуемся параметрическим представлением:

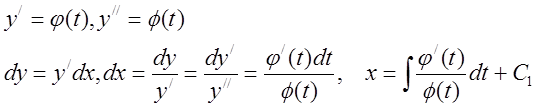
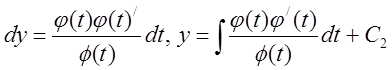
               III.                        .                                      (10)

 Понизить порядок можно заменой:  .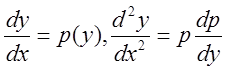

     Если уравнение (10) разрешимо относительно старшей производной , то помножим правую и левую часть на . Получим: 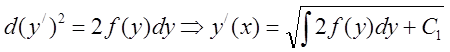 .Это уравнение с разделяющимися  переменными:.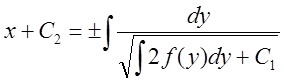

      Можно уравнение (10) заменить его параметрическим представлением: . Воспользуемся свойствами дифференциала:  .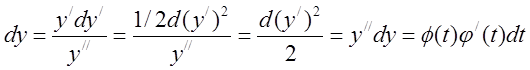

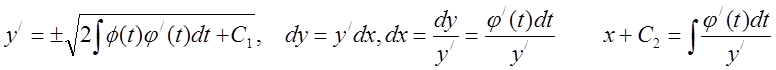Пример. .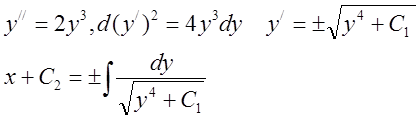

          Линейные дифференциальные уравнения n-ого порядка.

Определение. Линейными дифференциальными уравнениями n-го порядка называются уравнения вида: 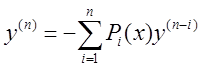 .                                                                                                                                                                 (1)  

Если коэффициенты  непрерывны на , то в окрестности любых начальных значений вида: , где  принадлежит интервалу, то в окрестности этих  начальных значений удовлетворяются условия теоремы о существовании и единственности. Линейность и однородность уравнения (1) сохраняется при любом преобразовании , где  - произвольная n раз дифференцируемая функция. Причем . Линейность  и однородность сохраняется при  линейном и однородном преобразовании неизвестной функции .

Введем линейный дифференциальный оператор: , тогда (1) можно записать так: . Определитель Вронского для  будет иметь вид:

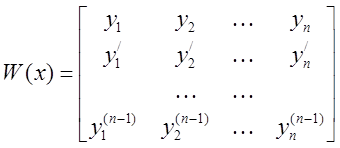, где - линейно независимые решения уравнения (1).