




Белорусский Государственный Университет Транспорта
кафедра «Высшая Математика»
Типовой расчёт
по математическому анализу
Выполнил:
студент группы ЭС-11
Пащенко В.А
Проверил:
преподаватель
Дудко С.А.
Гомель
2005.
Лабораторная работа №1
Решение алгебраических и тригонометрических уравнений.
Метод половинного деления:
Пусть функция F(x) непрерывна на [a;b]
и имеет в точках a и b разные
знаки, т.е. ![]() . Начальное приближение выбирают равным
. Начальное приближение выбирают равным 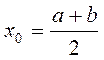 , т.е. делит отрезок пополам и выбирают его
середину. Если F(
, т.е. делит отрезок пополам и выбирают его
середину. Если F(![]() )=0, то
)=0, то ![]() – корень уравнения. В противном случае
выбирают тот отрезок из [a,
– корень уравнения. В противном случае
выбирают тот отрезок из [a, ![]() ][
][![]() ,b], на концах
которого F(x) имеет разные
знаки, т.к. корень лежит на этой половине.
,b], на концах
которого F(x) имеет разные
знаки, т.к. корень лежит на этой половине.
Если требуется точность ![]() , то деление пополам продолжают до тех пор,
пока длина отрезка не станет меньше 2
, то деление пополам продолжают до тех пор,
пока длина отрезка не станет меньше 2![]() . В этом случае середина
отрезка дает значение корня с точностью
. В этом случае середина
отрезка дает значение корня с точностью ![]() .
.
Программа на языке C++:
#include <stdio.h>
#include <math.h>
float e,a,b,x,y,ye;
void main()
{ a=0; b=5; y=999; ye=0; e=0.001;
while(fabs(y-ye)>e)
{ye=y;
x=(a+b)/2;
y=exp(0.724*x)-2.831*x;
if(y>0) b=x;
if(y<0) a=x;
if(y==0)
{y=0; ye=y;}}
fprintf(stdprn,"x=%f\n",x);
fprintf(stdprn,"y=%f\n",y);}
Результаты:
x=2.915344
y=0.000754
Лабораторная работа №2
Цель работы: представить тригонометрическим многочленом третьего порядка функцию F(x).
|
t |
p/6 |
p/3 |
p/2 |
2p/3 |
5p/6 |
p |
7p/3 |
4p/3 |
3p/2 |
5p/3 |
11p/6 |
2p |
|
F(t) |
2 |
4 |
3 |
30 |
30 |
10 |
5 |
10 |
20 |
25 |
30 |
20 |
Основные формулы:
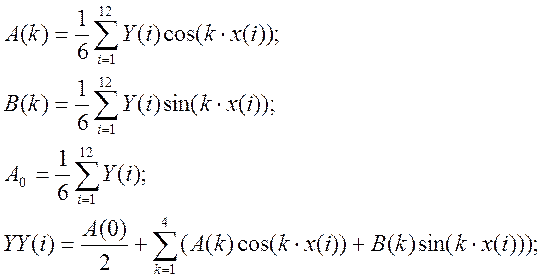
Программа на языке С++:
#include <stdio.h>
#include <math.h>
double x[]={0,M_PI/6,M_PI/3,M_PI/2,2*M_PI/3,5*M_PI/6,M_PI,7*M_PI/6, 4*M_PI/3,3*M_PI/2,5*M_PI/3,11*M_PI/6};
double y[]={-5,-10,-30,-30,-10,-5,-5,-5,-10,-30,-30,-30};
double ab(int k,int cos_or_sin) {
double s=0;
for(int i=0;i<12;s+=y[i]*(cos_or_sin?sin(k*x[i]):cos(k*x[i]))/6,i++);
return s; }
void main(void) {
double yy=ab(0,0)/2;
for(int k=4;k<=6;k++) {
printf("k=%d\n y(x)= yy(x)=\n",k);
for(int i=0;i<12;printf("%10.4f %10.4f\n",y[i],yy),yy=ab(0,0)/2,i++)
for(int n=1;n<=k;yy+=ab(n,0)*cos(n*x[i])+ab(n,1)*sin(n*x[i]),n++); }}
Результаты:
y(x) yy(x), k=3 yy(x), k=4
2.0000 5.4940 5.2440
4.0000 -2.6368 0.1132
3.0000 9.1890 6.6890
30.0000 27.5463 27.2963
30.0000 28.4450 31.1950
10.0000 12.9330 10.4330
5.0000 3.5060 3.2560
10.0000 9.6368 12.3868
20.0000 20.3110 17.8110
25.0000 26.4537 26.2037
30.0000 27.5550 30.3050
20.0000 20.5670 18.0670
Лабораторная работа №3
Цель работы: приближенное вычисление определенных интегралов методом трапеций и методом Симпсона.
Пусть требуется вычислить: 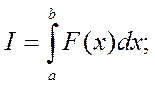
Если F(x)
непрерывна на отрезке [a;b], и
известна ее первообразная ![]() , то ее можно вычислить:
, то ее можно вычислить:
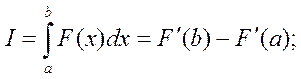
Метод трапеций:
|
|
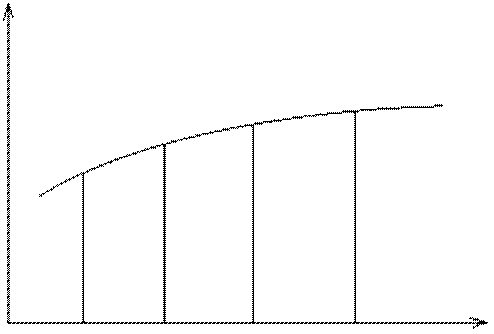 Основан на замене графика функции F(x) ломаной линией
Основан на замене графика функции F(x) ломаной линией ![]() .
.
Разобьем отрезок интегрирования на n разных частей:
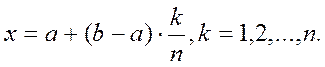
И с помощью прямых ![]() построить
n-трапеций. Сумма площадей их примерно равна S криволинейной трапеции aABb, т.е.
построить
n-трапеций. Сумма площадей их примерно равна S криволинейной трапеции aABb, т.е.
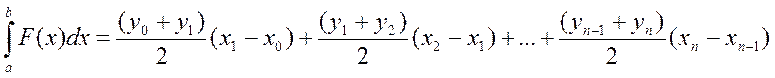 , где
, где ![]()
Упростив кривую часть приближенного равенства получим формулу трапеций:
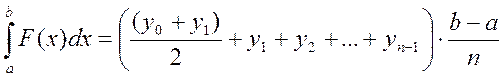
Погрешность измерения равна: 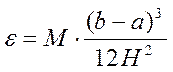
Метод Симпсона:
Основан на замене графика подинтегральной функции объединением парабол, оси которых параллельны оси Ox.
Для вычисления интеграла по методу Симпсона отрезок
интегрирования [a;b]
разбивается на 2r равных частей, где 2r
зависит от заданной точности ![]() :
:
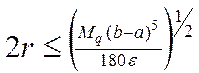 , где
, где ![]()
Вычисление интеграла проводится по формуле Симпсона.
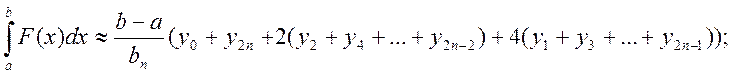
Программа на языке С++:
Для метода трапеций: Для метода Симпсона:
#include <iostream.h> #include <iostream.h>
#include <math.h> #include <math.h>
#define n 10 #define n 10
#define p 3.141592653589793238 #define p 3.141592653589793238
#define a 0 #define a 0
float y[10],h,b,c,xk[10],S,A=0; float y[30],h,b,c,xk[30],S,A=0,B=0;
int k; int k;
main() main()
{b=p/2; {b=p/2;
h=(b-a)/n; h=(b-a)/(2*n);
for (k=0;k<=n;k++) for (k=0;k<=2*n;k++)
{xk[k]=a+(k*h); {xk[k]=a+(k*h);
y[k]=sin(xk[k])/xk[k];} y[k]=sin(xk[k])/xk[k];}
for (k=1;k<=n-1;k++) A=A+y[k]; for (k=1;k<=(2*n)-1;k=k+2) A=A+y[k];
S=((b-a)/n)*((y[0]+y[n])/2+A); for (k=2;k<=(2*n)-2;k=k+2) B=B+y[k];
cout << S << endl; S=(h/3.)*(y[0]+y[n]+(4*A)+(2*B));
return 0;} cout << S << endl;
return 0;}
Результаты:
По методу трапеций интеграл равен: 1.291389
По методу Симпсона интеграл равен: 1.351486
Лабораторная работа №4
Решений дифференциальных уравнений методом Эйлера.
Мы будем рассматривать только дифференциальные уравнения
разрешенные относительно старшей производной, т.е. дифференциальные уравнения
вида ![]() Итак, пусть требуется решить
дифференциальное уравнение
Итак, пусть требуется решить
дифференциальное уравнение ![]() удовлетворяющее условию
удовлетворяющее условию![]() на отрезке
на отрезке ![]()
Разобьем отрезок на n равных
отрезков точками ![]() .
.
Приближенное решение получаем в виде множества чисел ![]() , где
, где ![]() -
при-ближенное значение искомой функции решения дифференциального уравнения в
точке
-
при-ближенное значение искомой функции решения дифференциального уравнения в
точке![]() .
.
Метод Эйлера:
В этом методе производная ![]() заменяется
приближенной формулой
заменяется
приближенной формулой 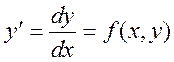
В результате на первом отрезке ![]() искомое
решение приближенного представляется функцией:
искомое
решение приближенного представляется функцией: 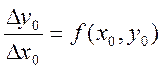 и
и ![]()
Аналогично находятся остальные приближенные значения.
![]() где
где ![]() для
для ![]()
Программа на языке С++:
#include <stdio.h>
#include <conio.h>
#include <math.h>
float f(float x, float y) Результаты:
|
|
|
|
|
0 1 2 3 4 5 6 7 8 9 10 |
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 |
0 0.100000 0.199942 0.298490 0.394327 0.486234 0.573154 0.654245 0.728900 0.796746 0.857622 |
{float t;
t=1+0.6*y*sin(x)-1.25*y*y;
return t;}
void main(void)
{int a=0,b=1;
float h=0.1,y[11],tt,i=0;
y[0]=0;
clrscr();
while (i<=1)
{i=i+0.1;
tt=f(i,y[i-1]);
y[i]=y[i-1]+h*tt;
printf("%f\n",y[i]);}}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.