Исследование сложной цепи постоянного тока (Лабораторная работа № 3), страница 2

  Потенциальная диаграмма строится следующим образом. Одну из точек цепи соединяют с землей. Потенциал этой точки принимают равным нулю, а потенциалы других точек вычисляются по формулам. Тогда

                                 

     Затем по оси абсцисс откладывают в масштабе сопротивления в том порядке, в котором они следуют друг за другом при обходе цепи, а по оси ординат откладывают также в масштабе величины значения потенциалов точек цепи. Поясним построение потенциальной диаграммы на примере.

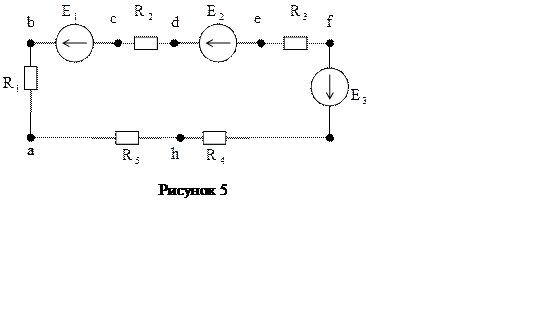
    Пример. Построить потенциальную диаграмму для цепи, если Е₁ =12В, Е₂ = 34В, Е₃ = 22В, R₁ = 5 Ом, R₂ = 4 Ом,     R₃ = 3 Ом, R₄ = 8 Ом, R₅ = 2 Ом (рисунок 5).

   Внутренним сопротивлением источника э.д.с. пренебрежем. Если направление обхода контура совпадает с направлением э.д.с. (от минуса к плюсу источника), то э.д.с. берется со знаком плюс, и со знаком минус – если не совпадает.

Решение. Определяем величину тока в цепи:

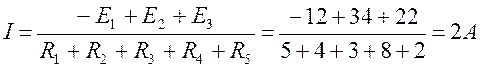
    Начнем обход цепи с точки а, потенциал которой равен нулю, т. к. она соединена с землей.

    При переходе от точки а в точку b проходим сопротивление R₁ в котором имеет место падение напряжения IR₁, т. е. , откуда потенциал  в точке b будет равен .

    Между точками b и с в цепи включен источник э.д.с. Разность потенциалов на его зажимах будет , откуда .

    Потенциал точки d ниже потенциала точки с на величину падения напряжения IR₂, т.е. , откуда . Если положительный заряд источника э.д.с. присоединен к точке е, а  отрицательный запишем – к точке d, то . Потенциал точки f ниже потенциала т. е. на величину падения напряжения IR₃, т. е. , откуда .

Потенциал точки g выше потенциала f  на величину э.д.с. Е₃, т. е. , откуда . Аналогично находим потенциал точки h , откуда  и конечная точка а , откуда .

По результатам полученных вычислений строим потенциальную диаграмму (рисунок 6).

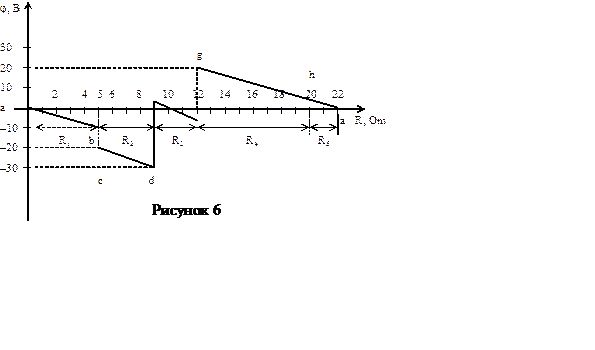1.5 Энергетический баланс в электрической цепи

    При протекании тока по сопротивлениям в последних выделяется тепло. На основании закона сохранения энергии, количество теплоты, выделяемое в единицу времени в сопротивлениях схемы (т. е. мощность) должна равняться энергии, доставляемой за тоже время источником питания. Уравнение энергетического баланса имеет вид

где Е - э.д.с. источника напряжения. U – разность потенциалов между узлами той ветви, в которой имеется источник тока с током I. При этом произведение входит со знаком плюс, если направление э.д.с. и ток через источник совпадает и со знаком минус – если не совпадает. Произведение берется со знаком плюс при условии, что величина U, равная разности потенциалов между узлами, к которым присоединяется источник тока, падение с учетом тока I (например, по методу узловых потенциалов).

2 Задание выполняемое при домашней подготовке

2.1  Изучить следующие методы расчета сложных цепей постоянного тока:

- I и II правила Кирхгофа;

- метод контурных токов;

- метод наложения.

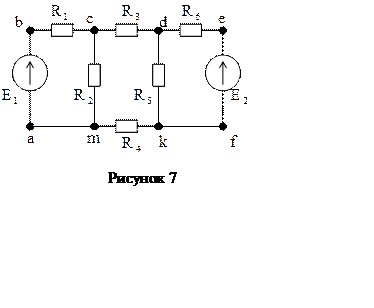
2.2  Рассчитать токи в ветвях схемы рисунка 7  по 1 и 2 правилам Кирхгофа, по методу контурных токов и методу наложения по заданным в таблице 1 параметрам схемы.  

                                                                                                                       Таблица 1