Статистический анализ экспериментальных данных методом наименьших квадратов (Раздел 8 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

Один из наиболее простых случаев тот, когда известно, что наблюдения некоррелированы и равноточны. В этом варианте корреляционная матрица вектора  или, что то же самое, вектора  выражается формулой

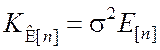                                                   ,                     (8.3.4)

где s² – дисперсия наблюдения; E_[n] – единичная матрица.

Дисперсия наблюдения может быть и неизвестной, тогда она подлежит оценке наряду с компонентами вектора A. При неизвестной дисперсии  s² не представляется возможным получить какие-либо характеристики точности оценивания.

Более общим является случай, когда наблюдения коррелированны и равноточны, однако для них известна только нормированная корреляционная матрица G_[n], а корреляционная матрица вектора  имеет вид

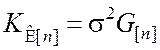                                                   ,                     (8.3.5)

причём s² – в общем случае неизвестная дисперсия наблюдения.

Покажем, что модель наблюдения (8.3.3), (8.3.4) легко сводится к модели (8.3.3), (8.3.5). Из линейной алгебры известно, что любая симметричная положительно-определённая матрица (а матрица G является таковой) может быть представлена в виде

                                                   ,                     (8.3.6)

где  – невырожденная матрица.

Произведём замену переменных по формуле

                                                      ,                         (8.3.7)

тогда

                                                        .                                    

Корреляционная матрица вектора  вычисляется следующим образом: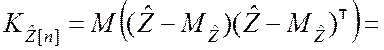                             

                       

                              

Получили выражение, аналогичное выражению  (8.3.4).

Условное уравнение (8.3.3) с учётом (8.3.7) приобретает вид

                                               .

Таким образом, модель наблюдения (8.3.3), (8.3.5) с помощью невырожденного линейного преобразования сводится  к соотношениям

                               ,    ,    .

Это и есть исходная модель наблюдения.

Если наблюдения коррелированы и неравноточны, то корреляционная матрица ошибок наблюдения

                                                     ,                       (8.3.8)

где  – известная симметричная положительно-определённая матрица, которая, как и матрица G в формуле (8.3.5), может быть представлена в виде произведения двух невырожденных квадратных матриц аналогично равенству (8.3.6). Это означает, что преобразованием, аналогичным преобразованию (8.3.7), модель наблюдения (8.3.3), (8.3.8) сводится к исходной модели.

По этим причинам в данном подразделе детально рассматривается только наиболее простая модель наблюдения (8.3.3), (8.3.4), а в конце его с помощью преобразования типа (8.3.6) получаются аналогичные результаты для схем наблюдения с корреляционными матрицами ошибок (8.3.5) и (8.3.8).

8.3.2. Нормальные уравнения и оценки наименьших квадратов

Для линейной модели наблюдения (8.3.1) квадратичная функция (8.2.6), при минимизации которой отыскиваются оценки компонентов вектора A, будет иметь вид

                                          ,             (8.3.9)

а нормальные уравнения (8.2.9) – вид

                                             .              (8.3.10)

Можно показать, что система нормальных уравнений (8.3.10) всегда совместна [10]. Будем считать, что матрица X имеет ранг k (предполагается, что n ³ k), а матрица весов Q – невырожденная. Тогда матрица  будет невырожденной, а потому из равенства (8.3.10) можно получить выражение для оценки вектора A:

                                             .             (8.3.11)

Если весовая матрица единичная (Q = E), то вместо соотношения (8.3.11) получим равенство