Методы статистического оценивания. Постановка задачи оценивания законов и параметров распределения случайных величин (Раздел 3 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

-  определение доверительной вероятности b_I,n (или b_e,n) при заданном доверительном интервале I (или максимальной вероятной погрешности e) и фиксированном объёме n выборки;

-  определение объёма n_b,I (или n_b,e) выборки, потребного для оценивания параметра a с требуемой надёжностью b  и точностью I (или e).

3.3. Оценивание вероятности случайного события

В результате реализации определённого комплекса условий  может произойти некоторое случайное событие , вероятность  появления которого неизвестна. Требуется по результатам наблюдений данного события  в некотором эксперименте оценить вероятность р.

Для решения поставленной задачи проводится серия n независимых и однородных испытаний – схема Бернулли, т.е. осуществляется n независимых реализаций одного и того же комплекса условий. Подсчитывается число m(A) = m испытаний, в которых событие A появилось. Отношение

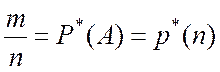                                                                 (3.3.1)

называется частотой события А в серии n испытаний или его статистической вероятностью. Проанализируем свойства частоты p^* как оценки вероятности p.

1. Поскольку число  появлений события А в n независимых и однородных испытаниях подчинено биномиальному закону распределения, то

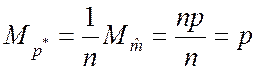                                            .              (3.3.2)

Из выражения (3.3.2) следует, что частота (3.3.1) является несмещённой оценкой вероятности p.

2. Согласно теореме Бернулли

                                    ,    ,

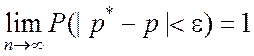т.е. частота p^* сходится по вероятности к вероятности р. Следовательно, рассматриваемая частота – это состоятельная оценка вероятности р.

3. Дисперсия частоты

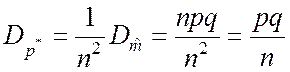                                          ,            (3.3.3)

где q = 1– p. Из соотношения (3.3.3) вытекает, что при n ® ¥ дисперсия  ® 0. Это означает асимптотическую эффективность указанной оценки. Можно показать, что при любом n дисперсия частоты - минимально возможная величина, следовательно, p^* является эффективной оценкой p.

Таким образом, частота p^* события А в серии n независимых однородных испытаний есть подходящее значение его вероятности, т.е. наилучшая точечная оценка.

Исследуем качество оценивания вероятности p по его частоте p^*. Итак, полагаем, что

                                                 .                             

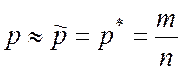Априори число  случайно и подчинено биномиальному закону распределения с параметрами n, p. Согласно теореме Муавра-Лапласа при достаточно больших n (практически при  np(1– p) > 9) биномиальное распределение может быть с достаточной точностью аппроксимировано нормальным распределением с параметрами ,  . В этом случае справедливо соотношение

       .                                                              

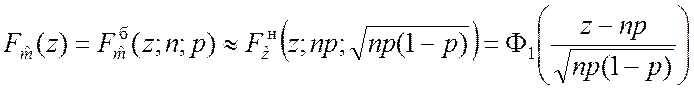Поскольку оценка  связана с  линейной зависимостью, она будет распределена приближённо нормально с параметрами

                                            .

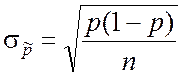Тогда справедливо

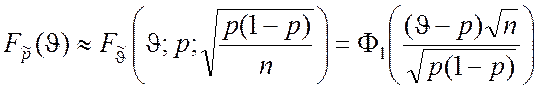                        .                                                         (3.3.4)

Так как закон распределения (3.3.4) оценки  симметричен относительно оцениваемой вероятности p, доверительный интервал I_b,n(p) будет симметричен относительно оценки . Для определения данного интервала достаточно знать половину его длины, которая равна максимальной с доверительной вероятностью b(p) абсолютной погрешности e(p):

                                              .

В результате доверительная вероятность для p будет определяться следующим равенством:

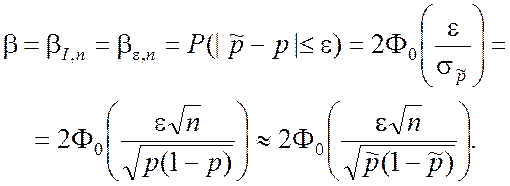                                                                                   (3.3.5)

Разрешив уравнение (3.3.5) относительно e, получим

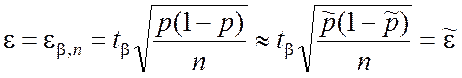                             , (3.3.6)

откуда

                       .                                                         (3.3.7)