Сценарии и анализ данных. Решение задач линейной оптимизации с помощью инструмента «Поиск решения». Решение нелинейных уравнений графическим методом и с помощью инструментов «Поиск решения» и «Подбор параметра», страница 2

3)  Вспомним алгебру, которую, надеюсь, учили в школе. Конкретно – как уравнения решаются графическим способом. Для этого одно уравнение перемещаем в левую часть, а второе – в правую. Далее приравниваем эти уравнения нулю и строим графики этих функций. Точка пересечения этих двух функций и будет корнем нелинейного уравнения. Их может быть даже два.

Преобразованные уравнения:

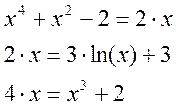
Стало гораздо легче, заметили? В каждом нелинейном уравнении у нас есть линейное уравнение, значит, решение графически способом будет не очень сложным.

3)  Решим первое нелинейное уравнение.

В ячейку B7 пишем – «Х»

В B8 – 1-е уравнение

В B9 – 2-е уравнение

В C7-K7 – координаты Х от -2 до 2

Примечание. Разумеется, можно взять и больший интервал координат. Но график тогда

будет слишком большим и неудобным. Для решения поставленной задачи хватит и (-2;2).

В C8 - =СУММ(СТЕПЕНЬ(C7;4);СТЕПЕНЬ(C7;2))-2

В C9 - =ПРОИЗВЕД(C7;2)

Далее выделяем ячейки С8 и С9, перемещаем курсор мыши в правый нижний угол, где он превратится в черный крестик. Удерживая левую кнопку мыши, перемещаем курсор мыши до ячейки К2.

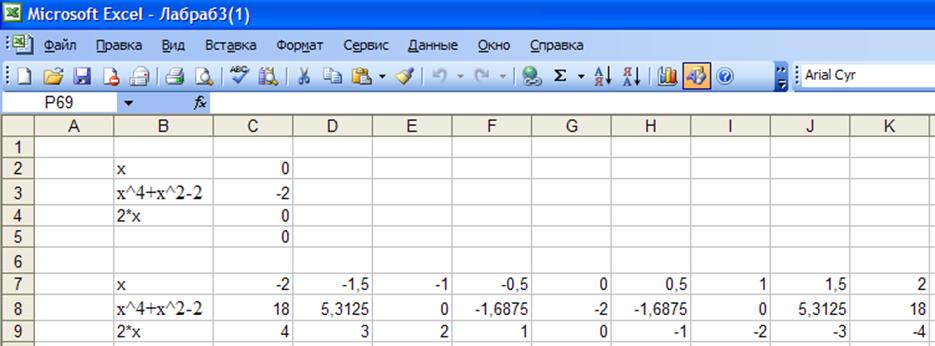
Рис. 16. Координаты Х и значения функций.

Программа автоматически высчитает значения уравнений. Но это только полдела. Выделяем все это безобразие и щелкаем на кнопке «Мастер диаграмм».

Там выберем тип диаграммы – «Точечная». И вид – Точечная диаграмма со значениями, соединенными сглаживающими линиями.

Примечание. Можно выбрать и другие типы диаграмм, но на точечной более наглядно.

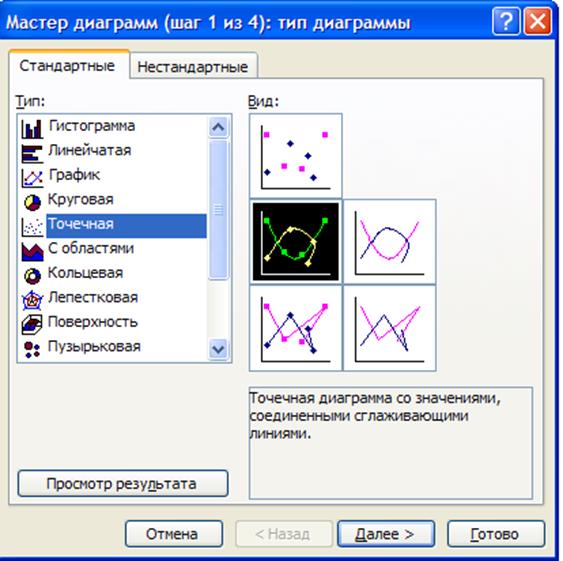
Рис. 17. Мастер диаграмм.

В результате у нас получится диаграмма:

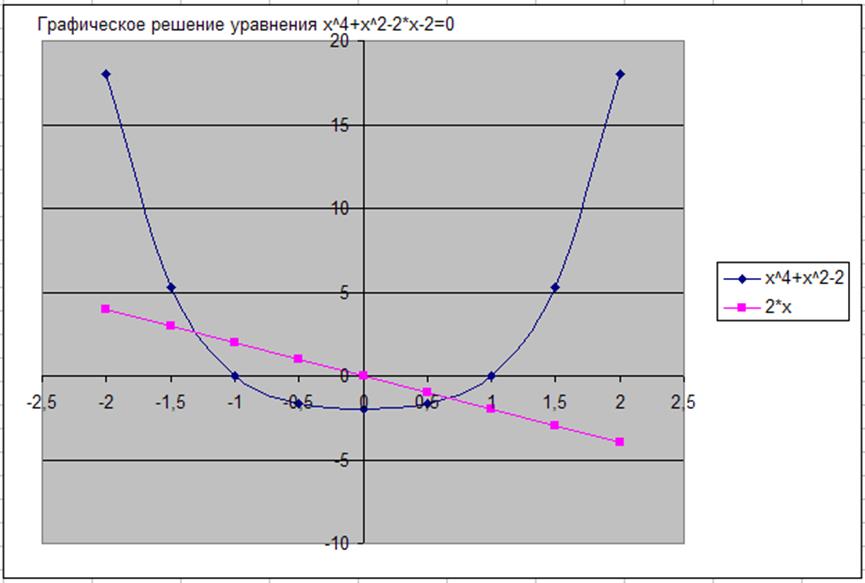
Рис.18. Полученная диаграмма.

Как видно, есть две точки пересечения, но эти точки довольно сложно увидеть. Поэтому выделяем два интервала, в котором находятся корни – (-1;0,5) и (1;1,9) .

И повторяем сделанное ранее, но в качестве координат Х выбрать уже другие интервалы.

Рис.13-14. Интервалы, в которых находятся корни.

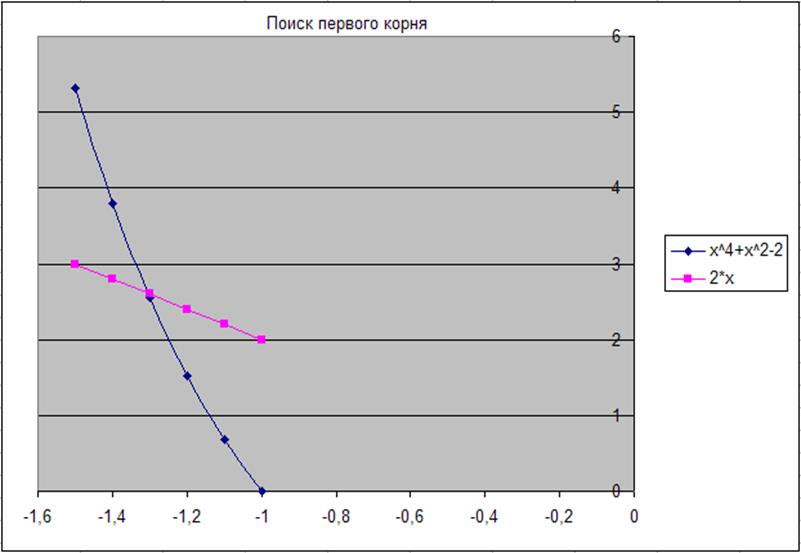
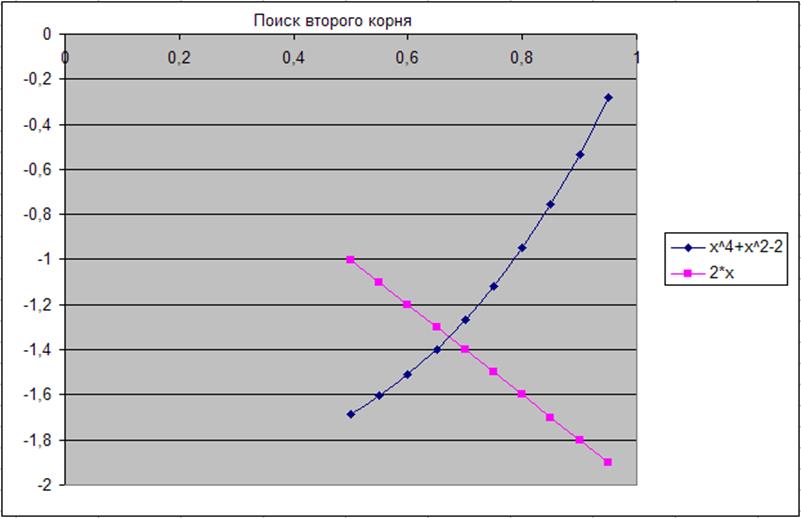
Рис. 19-20. Результаты приближений.

Как видно из диаграмм, корни Х: х1=-0,7;х2=1,3. Всё.

Далее повторяем все операции, описанные выше, для второго и третьего уравнений.

2) Но в С8 пишем – Х,

В С9 - =ПРОИЗВЕД(C8;2),

С10 - =ПРОИЗВЕД(3;LN(G8))+3.

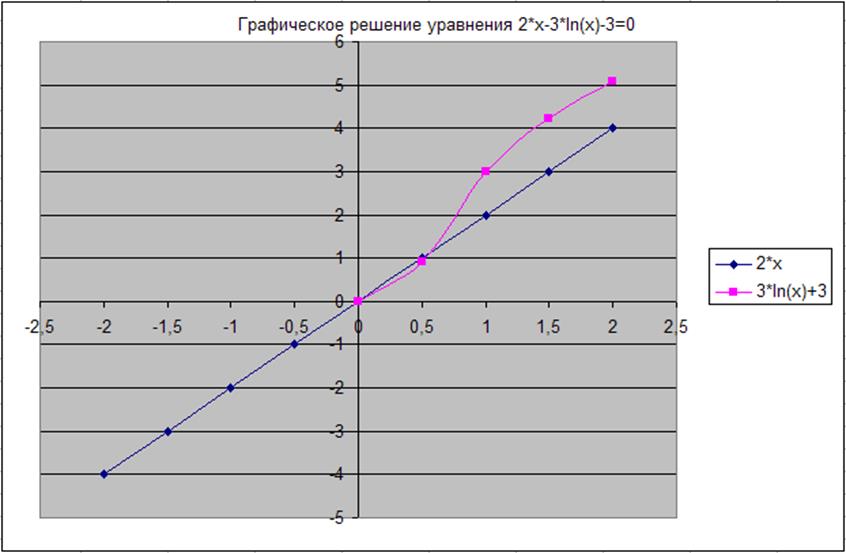
Рис. 22. Решение второго уравнения.

В данном случае корень только один и он очевиден – х=0,5.

Но сделаем приближение и для этого случая.

Рис. 23. Интервал, содержащий корень.

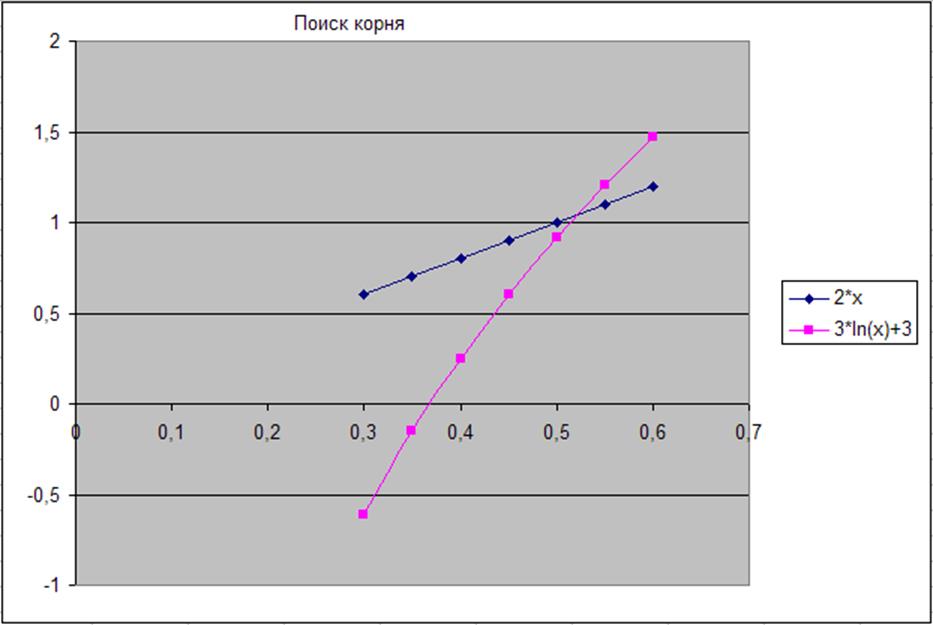
Рис. 24. Приближение.

Как мы видим, х=0,52. И здесь мы впервые осознаем, что все решения, сделанные с графическим способом, находят не точные корни, а лишь приблизительные, «на глаз».

3) На этот раз пишем в С9 - =ПРОИЗВЕД(4;C8)

В С10 - =СТЕПЕНЬ(C8;3)+2.

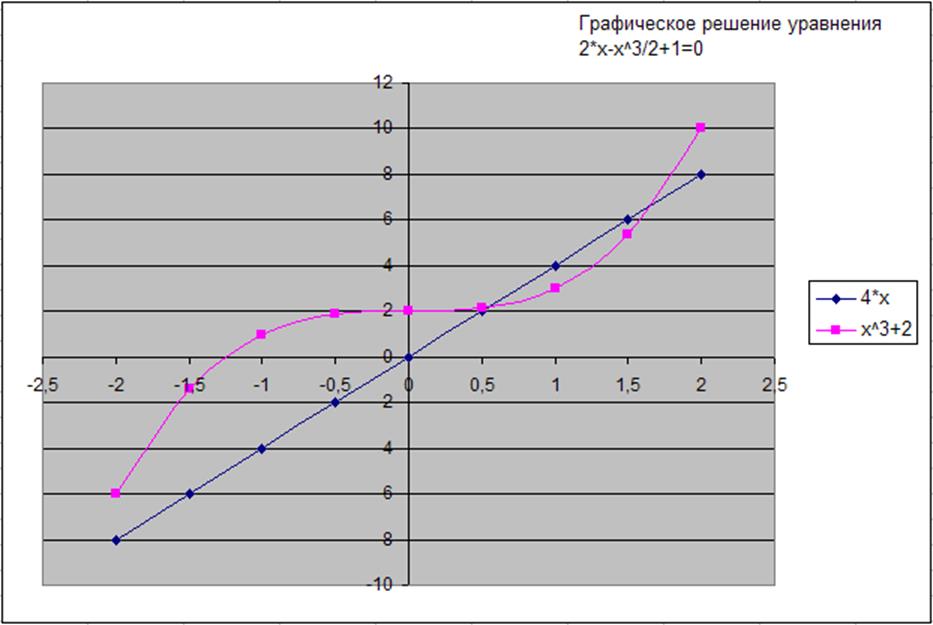
Рис. 25. Решение третьего уравнения.

Делаем приближения.

Рис. 26-27. Приближения.

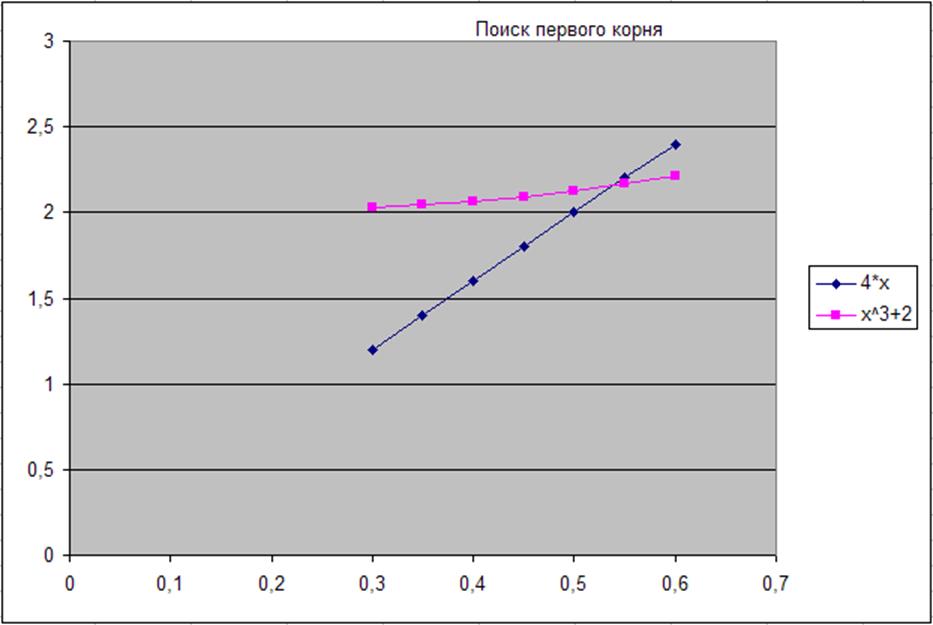
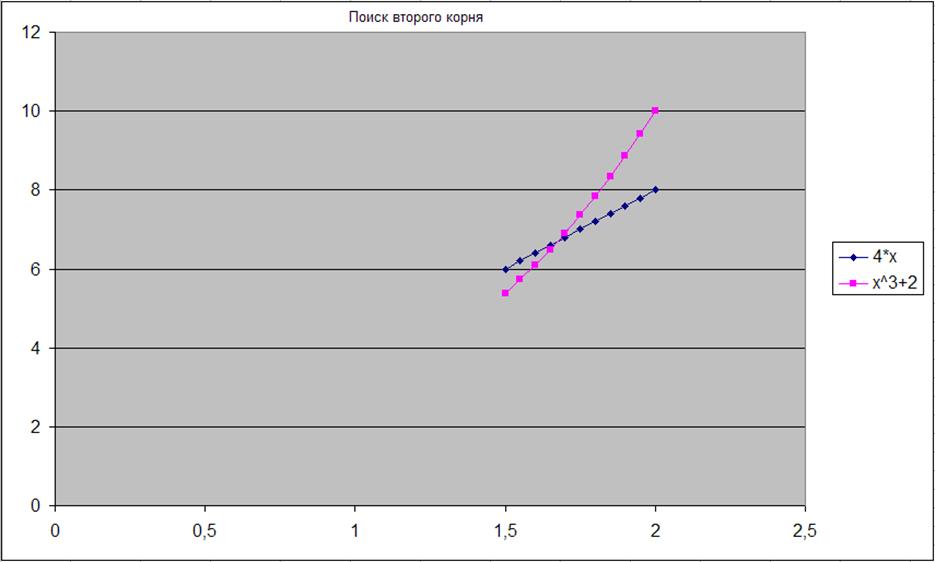
Рис.28-29. Результаты приближений.

Как видно, х1=0,55;х2=1,7.

2) С помощью инструмента «Поиск решения» решение нелинейных уравнений упрощается в несколько раз. Смотрим первое изображение.

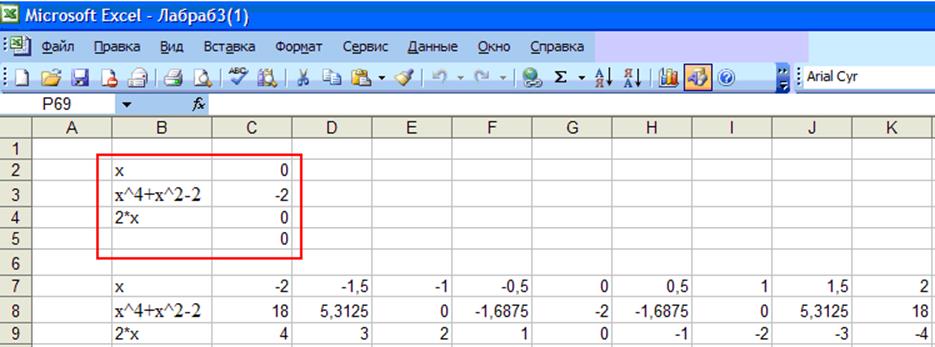
Рис. 30.

Заполняем ячейки так, как показано на рисунке. В С2 пишем – 0.

В С3 - =СУММ(СТЕПЕНЬ(C2;4);СТЕПЕНЬ(C2;2))-2;

В С4 - =-ПРОИЗВЕД(C2;2);

В С5 - =С2. Это будет целевая функция.

Поехали.

Далее открываем меню СЕРВИС/ПОИСК РЕШЕНИЯ.

Ставим одно-единственное ограничение – С3=С4. Поскольку в математике возможны любые числа.

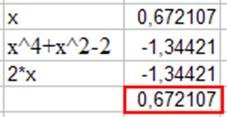
Рис. 31.

Вот что мы получили на выходе. Первый корень получен. Причем гораздо более точное, чем наша оценка «на глаз».

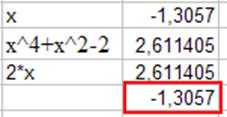
Рис. 32.

Для получения второго корня мы добавляем новое ограничение – С2<=0.

А напоследок. Может оказаться, что оба корня будут лежать в одной четверти и решение корня может оказаться проблематичным. Для решения этой проблемы есть максимальное и минимальное значение целевой функции.

Обратите внимание, что в третьем уравнении надо ввести ограничение С2>=0, чтобы найти второй корень.

Со вторым уравнением проблем быть не должно, так как корень только один.

3) Для того, чтобы воспользоваться инструментом «Подбор параметра», НУЖНО знать искомое значение. Немного странно, не правда ли? Поскольку мы уже нашли решение уравнений двумя способами, воспользуемся третьим способом для проверки. Рассмотрим этот способ на примере третьего уравнения.

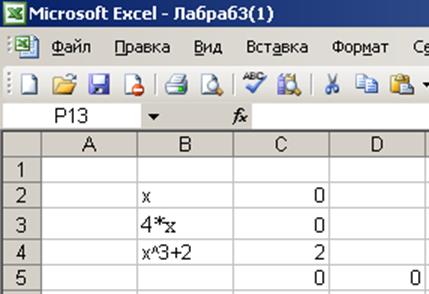
Рис. 33. Подбор параметра.

Рядом с ячейкой целевой функции нужно поместить ее дубликат. В D5 пишем формулу =C2. Далее СЕРВИС/Подбор параметра.

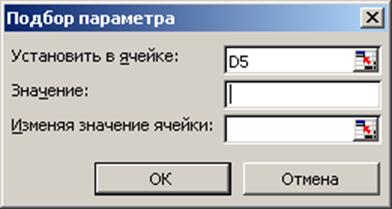
Рис. 34.

Пишем в поле «Значение» значение искомого параметра. А в поле «Изменяя значение ячейки» ставим С2. Нажимаем кнопку «ОК».

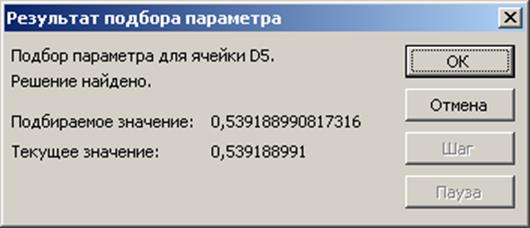
Рис. 35.

Вот и все. Всем спасибо за внимание.

Результаты использования трех различных способов.

Уравнения	Графический метод	Поиск решения	Подбор параметра
	х1=0,7; х2=-1,3	x1=0,672107; x2=-1,3057	x1=0,672107; x2=-1,3057
	х=0,5	x=0,52	x=0,52
	х1=0,55; х2=1,7	x1=0,539188; x2=1,67513	x1=0,539188; x2=1,67513

Часть III.

Заключение.

 В данной лабораторной работе мы освоили три различных способа решения нелинейных уравнений: графический, инструменты «Поиск решения» «Подбор параметра». Экспериментальным путем было установлено, что лучший способ: «Поиск решения». Хоть и не особо впечатляющий, но эффективный и быстрый способ.

  Так же мы рассмотрели решение задач нелинейной оптимизации. Для этого опять же рассмотрели инструмент «Поиск решения» и один из мощнейших инструментов – сценарии.