




Лекция 6
Энергия электростатического поля
|
|
Любому объему пространства, в котором существует электрическое поле, может быть сопоставлена энергия, величина которой пропорциональна произведению квадрата поля на этот объем. При вычислении энергии, запасенной в поле точечного заряда, возникают существенные трудности в теории, которые, по-видимому, носят принципиальный характер. |
6.1. Энергия системы точечных зарядов
В соответствии с общим определением потенциальной энергии системы взаимодействующих тел электростатической энергией системы зарядов следует назвать работу, которую было бы необходимо совершить против сил поля при “сборке” этой системы в процессе перемещения зарядов из бесконечности в точки их истинного расположения. Электростатическая энергия системы неподвижных зарядов равна половине суммы произведений величин этих зарядов на потенциалы, создаваемые в точках их нахождения всеми остальными зарядами системы (6.1).
Для доказательства сделанного утверждения удобно воспользоваться методом математической индукции. Для случая двух зарядов справедливость формулы (6.1) достаточно очевидна (6.2). При осуществлении индукционного перехода необходимо учесть, что введение в систему из N зарядов N+1 заряженной частицы приведет к изменению потенциалов во всех точках нахождения ранее имевшихся зарядов. При этом истинность индукционного перехода доказывается цепочкой равенств (6.3).
Естественное обобщение формулы (6.1) на случай непрерывного распределения зарядов приводит к более удобному в практическом использовании соотношению (6.4).
|
|
(6.1) |
Энергия системы неподвижных точечных зарядов. |
|
|
(6.2) |
База для индукционного перехода (N=2). r12 - расстояние между зарядами с соответствующими номерами. |
|
|
(6.3) |
Индукционный переход для доказательства (6.1). ji (N) - потенциал, создаваемый в точке нахождения i-заряда всеми остальными N зарядами, кроме него самого. |
|
|
(6.4) |
Обобщение формулы (6.1) на случай непрерывного распределения зарядов. |
6.2. Энергия системы заряженных проводников
В случае системы заряженных проводников выражение для электростатической энергии (6.1) или (6.4) существенно упрощаются из-за того, что объем любого проводника эквипотенциален. В результате вместо вычисления суммы по гигантскому числу точечных зарядов qi (или интегрирования) оказывается достаточным выполнить аналогичное суммирование только по изолированным друг от друга проводникам, несущими суммарные заряды QJ
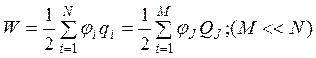 .
.
В случае уединенного проводника потенциал его поверхности оказывается пропорциональным величине заряда. Действительно, пусть имеющий заряд Q проводник заданной формы создает в пространстве распределение потенциала j (r). На поверхности проводника эта функция имеет постоянное значение j0. Рассмотрим новое распределение потенциала f(r)=a j(r)., отличающееся от исходного умножением на константу, при котором потенциал поверхности проводника увеличивается в a раз. Во столько же раз увеличится и его градиент, а следовательно и напряженность поля во всех точках пространства, в том числе и около поверхности проводника. Последнее означает пропорциональное возрастание поверхностного распределения заряда проводника и, следовательно, его полного заряда. Из теоремы единственности решения задач электростатики следует, что увеличение заряда проводника в a раз обязательно приведет к рассмотренному распределению потенциала.
Отношение величины заряда проводника к потенциалу его поверхности носит название емкости (6.6). Величина емкости проводника не зависит от его заряда и определяется только формой его поверхности. С учетом определения емкости (6.6) выражение для электростатической энергии уединенного проводника может быть переписано в виде (6.7).
В случае системы проводников потенциал в произвольной точке пространства (в том числе и самих проводников) является линейной комбинацией зарядов всех проводников (6.8). Коэффициенты линейной комбинации называются потенциальными коэффициентами и составляют матрицу с размерностью, равной числу проводников. Элементы обратной ей матрицы называют емкостными коэффициентами (6.9). Обе матрицы оказываются симметричными относительно их диагоналей. С учетом определений (6.9) энергия системы проводников может быть записана как квадратичная форма от их зарядов или потенциалов (6.10).
Систему из двух имеющих равные разноименные заряды проводников, потенциалы которых не зависят от внешних зарядов, называется конденсатором. Разность потенциалов между образующими его проводниками - обкладками - является линейной функции величины заряда (6.11). Соответствующий коэффициент пропорциональности (6.12) носит название емкости конденсатора. Энергию заряженного конденсатора можно рассчитать как работу по перенесению заряда Q малыми порциями с одной пластины на другую.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.