![]() , (12.23)
, (12.23)
где
![]() - матрица преобразования Лоренца.
Преобразование (12.23) получается как преобразование произведения двух 4 –
векторов
- матрица преобразования Лоренца.
Преобразование (12.23) получается как преобразование произведения двух 4 –
векторов ![]() и
и ![]()
![]() ,
, ![]() .
.
В
качестве примера применим (12.23) для вывода преобразования компоненты поля ![]() . Формула преобразования имеет вид
. Формула преобразования имеет вид
![]() .
.
Учитывая,
что ![]() , получим
, получим ![]() .
Поэтому
.
Поэтому
![]() ,
,
где
![]() . Приходим к формуле преобразования
. Приходим к формуле преобразования
![]() .
.
Аналогично
получаются формулы преобразования для других компонент поля. Формулы
преобразования удобно записывать в векторной форме, для этого поля разобьем на
составляющие, параллельные и перпендикулярные направлению движения системы ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Учитывая,
что ![]() , получаются формулы
, получаются формулы
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Формулы
обратного преобразования получаются заменой величин со штрихом на
соответствующую величину без штриха и наоборот, а так же изменением знака у ![]() .
.
Рассмотрим две предельные ситуации.
1.).
В системе ![]() отсутствует магнитное поле
отсутствует магнитное поле ![]() . В системе
. В системе ![]() будет и
электрическое поле и магнитное:
будет и
электрическое поле и магнитное:
![]() ,
,
![]() .
.
Последнее
равенство показывает, что поля ![]() и
и ![]() ортогональны. Следует отметить, что эту
ортогональность можно обнаружить не делая преобразований. В самом деле,
скалярное произведение
ортогональны. Следует отметить, что эту
ортогональность можно обнаружить не делая преобразований. В самом деле,
скалярное произведение ![]() является инвариантом, а в
рассматриваемом примере
является инвариантом, а в
рассматриваемом примере ![]() и значит
и значит ![]() , т.е.
, т.е. ![]() и
и ![]() - ортогональны.
- ортогональны.
2.).
В системе ![]() отсутствует электрическое поле
отсутствует электрическое поле ![]() . В системе
. В системе ![]() будет и
электрическое поле и магнитное, можно сразу отметить, что :они будут
ортогональны
будет и
электрическое поле и магнитное, можно сразу отметить, что :они будут
ортогональны
![]()
![]() .
.
С
учетом последнего соотношения можно переписать выражение для поля ![]() в виде
в виде
![]() , где учтено, что
, где учтено, что ![]() .
.
12.10. Релятивистская 4 – сила Лоренца. Плотность трехмерной силы Лоренца (сила, действующая на заряды в единичном объеме среды) определяется формулой
![]() ,
,
где
![]() - скорость заряженной среды и плотность
зарядов.
- скорость заряженной среды и плотность
зарядов.
Обобщение
на четырехмерный случай делается следующим образом. Ранее введены понятия: 4 –
вектор тока ![]() и тензора электромагнитного поля
и тензора электромагнитного поля ![]()
Введем в рассмотрение 4 – вектор
![]() .
.
Выпишем компоненты этого 4 – вектора (он называется плотностью силы Лоренца)
![]() ,
,
где
учтено соотношение ![]() .
.
Аналогично находятся остальные три компоненты
![]() ,
,
![]() ,
,
![]() .
.
Первые три компоненты совпадают с соответствующими компонентами трехмерной плотности силы Лоренца. Сделаем преобразование:
![]()
![]() ,
,
поэтому
можно ![]() (это сила Минковского) представить в виде
(это сила Минковского) представить в виде
![]() .
.
В
частном случае сопутствующей системы отсчета ![]() заряды неподвижны
заряды неподвижны
![]() и в системе
и в системе ![]() будем
иметь
будем
иметь ![]() :
:
![]() .
.
Введенная 4 – плотность силы Лоренца позволяет написать четырехмерное релятивистское уравнение движения заряженной среды
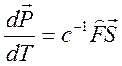 ,
,
где
![]() - собственное время,
- собственное время, ![]() - 4 – импульс.
- 4 – импульс.
12.11. Тензорная форма уравнений Максвелла. Уравнения Максвелла в трехмерной формулировке возьмем в виде
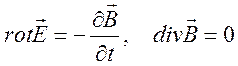 , (12.24)
, (12.24)
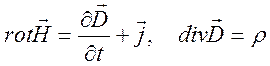 , (12.25)
, (12.25)
Для
записи уравнений (12.24) в тензорной форме, вместо тензора электромагнитного
поля ![]() удобнее использовать дуальный тензор
удобнее использовать дуальный тензор ![]() , который отличается от
, который отличается от ![]() заменой компонент
заменой компонент ![]() на
на
![]()
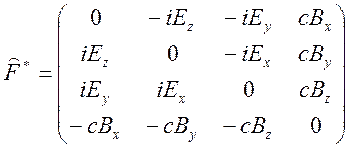 .
.
В результате система (12.24) приводится к тензорной форме
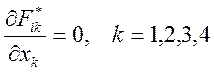 .
.
Принимая
во внимание вид тензора индукции ![]() (12.22.А) , система
(12.25) приводится к тензорной форме
(12.22.А) , система
(12.25) приводится к тензорной форме
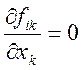 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.