Решение задачи Коши

Notrecognized

Ответ: Пусть некоторая область в . Она называть ее конфигурационным пространством.

Полем направлений в называется семейство прямых, такое, что каждой точке поставлена в соответствие некоторая прямая данного семейства, которая проходит через точку .

Интегральными кривыми заданного поля направлений называются гладкие кривые, касательные к которым в каждой точке совпадают с соответствующими прямыми поля направлений.

Введем декартовы координаты в области . Прямая однозначно задается точкой, через которую она проходит, и направляющим вектором. Предполагая, что среди прямых поля нет перпендикулярных к оси , условимся направляющий вектор нормировать так, чтобы его первая координата была равна единице. Этим условием направляющий вектор будет определен однозначно. Если теперь прямая поля направлений соответствует точке с координатами , то ее направляющий вектор как функция этой точки запишется в виде или, кратко, 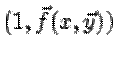. Направляющий вектор касательной к кривой в той же точке будет равен . Равенство данных направляющих векторов и ведет к дифференциальному уравнению

Таким образом, с геометрической точки зрения, решить задачу Коши -- это найти интегральную кривую заданного поля направлений, проходящую через данную точку.

Ответ:

Рассмотрим задачу Коши

Зададим положительное число , называемое далее шагом. Проведем через точку 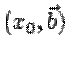прямую поля направлений, определенную дифференциальным уравнением, и отложим от начальной точки отрезки длиной в шаг. Взяв одну из двух полученных точек (мы считаем, что шаг достаточно мал и процедура не выводит нас за пределы конфигурационного пространства), проведем через нее прямую поля направлений и отложим на ней отрезок длиной в шаг таким образом, чтобы угол между отрезками был тупым. Повторим эту операцию некоторое число раз. Аналогично поступим и с другой точкой в шаге от начальной. Описанная процедура приводит нас к ломаной, которая называется ломаной Эйлера (сделайте рисунок). Если шаг достаточно мал, мы смеем надеяться, что полученная кривая в своих гладких точках мало отличается от искомой интегральной кривой. Устремляя шаг к нулю, мы хотели бы получить саму интегральную кривую.

Оказывается, что такого предела вообще говоря нет. Однако можно показать, что:

если функция непрерывна в окрестности начальной точки, то из любой последовательности ломаных Эйлера с убывающим к нулю шагом в некоторой окрестности начальной точки существует подпоследовательность, сходящаяся к гладкой кривой, которая является интегральной. В частности, при наложенном условии решение задачи Коши существует. Это утверждение составляет содержание теоремы Пеано.