Пространство состояний (State-Space). Линейные системы с сосредоточенными параметрами (line and time-invariant system – LTI)

Пространство состояний (State-Space) – один из способов описания модели с помощью системы дифференциальных уравнений первого порядка. Пространством состояний называют минимальный набор функций , достаточный для полного описания модели. У системы может быть набор входных параметров  и набор выходных параметров , где n – порядок системы или размерность пространства состояний, r – размерность вектора входных параметров, m – размерность вектора выходных параметров. Для однозначного описания модели необходимо задать состояние системы в начальный момент времени  и зависимость от времени всех входных параметров модели в последующие моменты времени .

Рис. 1 Блок-схема модели.

Система из n обыкновенных дифференциальных уравнений первого порядка, описывающая поведение модели, в общем виде может быть записана как 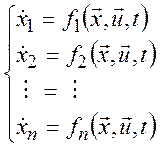(1)

                                                                                                                                             (1)

где  – некоторые функции от величин, описывающих состояние системы, входных параметров и времени. Производные по времени находятся только в левой части уравнений. Для краткости введены следующие обозначения:

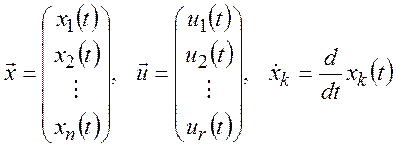                                                                                                                         (2)

Систему (1) называют уравнения состояния, а вектор  – вектор состояний. С помощью системы уравнений состояния (1) можно описывать как линейные, так и нелинейные модели.

Линейные системы с сосредоточенными параметрами (line and time-invariant system – LTI) описываются системой линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами. В этом случае функции  должны линейно зависеть от  и . Тогда общий вид системы (1):

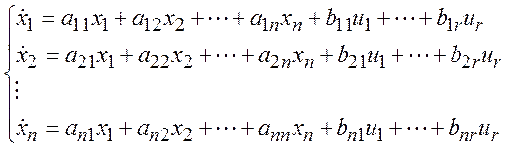                                                                                                                (3)

где  и  константы, описывающие систему. Уравнения (3) могут быть записаны в матричной форме:

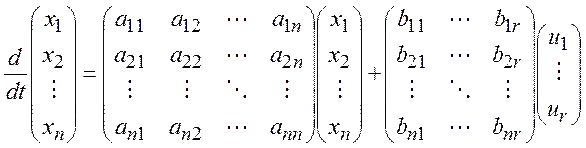                                                                                                       (4)

или в более компактном виде:

                                                                                                                                                (5)

где A и B обозначают соответствующие матрицы в (4). Размерность матрицы A , матрицы B .

Выходными параметрами модели может быть любой набор величин, представляющий интерес. При этом для описания модели в терминах пространства состояний могут быть выбраны другие величины, отличные от тех, которые выбраны как выходные параметры модели. Выходные параметры выражаются через вектор состояний и входные параметры с помощью системы уравнений для выходных параметров. В случае линейной системы с распределёнными параметрами уравнение для выходных параметров также будет линейным с постоянными коэффициентами, которое можно записать в матричной форме:

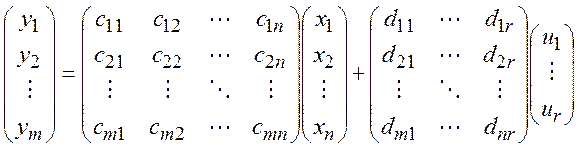                                                                                                        (6)

где  и  константы. Уравнения (6) в компактной форме:

                                                                                                                                               (7)

Размерность матрицы C – , матрицы D – .

Полная система уравнений для линейной системы с сосредоточенными параметрами состоит из уравнения состояния (5) и уравнения для выходных параметров (7). Матрицы A и B определяются структурой системы и её элементами, а матрицы C и D – выбором выходных параметров.

Целиком процедура моделирования состоит из следующих этапов:

1.  определить порядок системы n и выбрать набор величин , описывающих состояние системы.

2.  Составить систему уравнений состояния, то есть найти матрицы A и B.

3.  Подобрать матрицы C и D, чтобы выразить интересующие выходные параметры через вектор состояния  и входные параметры .

Пример 1

Написать уравнение состояния для дифференцирующей цепочки. Входным параметром будет напряжение, подаваемое на вход цепочки, выходным параметром падение напряжения на сопротивлении (рис. 2).

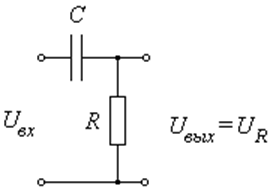
Рис. 2 Дифференцирующая цепочка.

Пусть R = 10кОм, C = 1мкФ, тогда RC = 0.01с, нулевые начальные условия, то есть до возникновения входного сигнала, напряжение на обкладках конденсатора равно нулю.

Сначала определяем порядок системы и подбираем минимальный набор величин для задания состояния системы. Уравнения состояния содержат в левой части первые производные по времени, поэтому в качестве величин, описывающих состояние системы, удобно выбрать те, которые являются интегралом по времени от другой величины. В данном примере это напряжение на конденсаторе , которое выражается через интеграл от тока I. Через конденсатор и сопротивление течёт одинаковый ток, так как они включены последовательно.

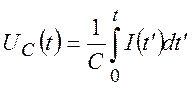                                                                                                                                          (8)

Запишем всё в обозначениях, в которых написана формула (5). Входной параметр , вместо вектора состояния будет скаляр, так как у дифференцирующей цепочки только одна величина выражается как интеграл по времени, поэтому , выходной параметр . Ток может быть выражен через падение напряжения на сопротивлении по закону Ома.