Математика \ Математический анализ

Ответы на контрольные задания по теме: "Криволинейные интегралы на плоскости"

Страницы работы

8 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Криволинейные интегралы на плоскости

Ответ: 1

Гладкая кривая на плоскости или в пространстве задается параметрически. Параметризованная кривая иначе называется путем и представляет собой гладкое отображение отрезка, соответственно, на плоскость или в пространство. Под кривой при этом понимается множество всех путей, имеющих один и тот же образ. Если $\gamma (t)$ -- некоторый путь, то его производная $\gamma' (t)$ называется скоростью пути. Путь называется гладким, если его скорость нигде не обращается в ноль. Кривая называется гладкой, если среди ее параметризаций есть гладкий путь.

Пусть $\gamma (t)$ -- параметризация некоторой кривой $\Gamma$ . Касательным вектором к кривой $\Gamma$ в точке $P=\gamma (t)$ называется любой вектор, коллинеарный вектору скорости $\tau (P)=\gamma' (t)$ в этой точке. В каждой точке гладкой кривой определена пара взаимно противоположных единичных касательных векторов:

$\displaystyle P=\gamma (t)\,,\qquad \tau (P)=\pm \frac{\gamma' (t)}{ \vert\gamma' (t)\vert}\,.$

Это определение не зависит от выбора параметризации кривой.

Ответ: 2

Гладкая кривая $\Gamma$ на плоскости или в пространстве задается параметрически как образ некоторого гладкого пути $\gamma (t),\;t\in[a,b]$ , в координатном виде (в пространстве):

$\displaystyle x=x (t) ,\quad y=y(t) ,\quad z=z (t) .$

Путь $\gamma (t)$ эквивалентен пути $\alpha (s) ,s\in[c,d]$ , если $\gamma (t)=\alpha (\varphi (t))$ , где $\varphi$ -- гладкая функция, производная которой нигде не обращается в ноль. Этим отношением пути, параметризующие кривую $\Gamma$ , делятся на два не пересекающихся класса, каждый из которых состоит из эквивалентных между собой путей и называется ориентированной кривой. Выбор ориентированной кривой и называется ориентацией данной кривой. Ориентацию кривой можно определить выбором одного из двух единичных касательных векторов

$\displaystyle \pm\frac{\gamma' (t)}{\vert\gamma' (t)\vert} ,$

непрерывно зависящих от точки $\gamma (t)$ кривой. Если кривая не замкнута, ее ориентацию можно задать выбором начала и конца кривой (упорядочением концов). Ориентация составной (кусочно гладкой) кривой определяется тем условием, что начало каждого следующего куска кривой должно являться концом предыдущего.

Ответ: 4

Пусть $\Gamma$ -- гладкая кривая с параметризацией $\gamma (t),\;t\in[a,b]$ . Пусть, далее, -- непрерывная вещественнозначная функция, определенная на $\Gamma$ . Интеграл

$\displaystyle \int\limits_{\Gamma}f\,dl\overset{\text{Опр.}}=\int\limits_{a}^{b}f (\gamma (t))\vert\gamma' (t)\vert\,dt$

не зависит от параметризации кривой и называется криволинейным интегралом 1 рода или интегралом по длине дуги. В частности, интеграл от даст длину кривой $\Gamma$ . В координатном виде

$\displaystyle \gamma (t)= (x (t),y (t),z (t))\,,\qquad\vert\gamma' (t)\vert= \sqrt{x'^{2} (t)+y'^{2} (t)+z'^{2} (t)}\,.$

Физический смысл интеграла 1 рода заключен в следующем. Если $\rho$ -- линейная плотность тонкой тяжелой проволоки формы $\Gamma$ , то масса проволоки определяется интегралом

$\displaystyle M= \int\limits_{\Gamma}\rho\,dl\,.$

Ответ:6

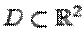Простая гладкая поверхность $\Gamma$ задается параметрически как образ гладкого отображения $\theta:\;D\to \mathbb{R}^{3}$ плоской области $D\subset \mathbb{R}^{2}$ при условии, что ранг производной (матрицы Якоби) отображения $\theta$ равен 2. Переменные на называются локальными координатами на поверхности $\Gamma$ .

Под площадью поверхности $\Gamma$ понимают интеграл

$\displaystyle S (\Gamma)= \iint\limits_{D} \sqrt{\det (\theta'^{T}\theta')}\, dudv\,,$

где $\theta'^{T}$ -- матрица, транспонированная к матрице Якоби $\theta'$ . В координатном виде

$\displaystyle \det(\theta'^{T}\theta')=\left( \frac{D (y,z)}{D (u,v)} \right)^{... ...)}{D (u,v)} \right)^{2}+ \left( \frac{D (x,y)}{D (u,v)} \right)^{2}=EG-F^{2}\,,$

где

$\displaystyle E$	$\displaystyle =\left\vert \frac{\partial\theta}{\partial u} \right\vert^{2}= \l... ... y}{\partial u} \right)^{2}+ \left(\frac{\partial z}{\partial u} \right)^{2}\,,$
$\displaystyle F$	$\displaystyle = \frac{\partial\theta}{\partial u} \cdot \frac{\partial\theta}{\... ...\partial v}+ \frac{\partial z}{\partial u}\cdot\frac{\partial z}{\partial v}\,,$
$\displaystyle G$	$\displaystyle =\left\vert \frac{\partial\theta}{\partial v} \right\vert^{2}= \l... ... y}{\partial v} \right)^{2}+ \left(\frac{\partial z}{\partial v} \right)^{2}\,.$

В случае явного задания поверхности

$\displaystyle S (\Gamma) = \iint\limits_{D} \sqrt{1+ \left( \frac{\partial g}{\partial x} \right)^{2}+ \left(\frac{\partial g}{\partial y} \right)^{2}}\,dxdy\,.$

Ответ:7

Пусть $\Gamma$ -- простая гладкая поверхность с параметризацией $\theta:\;D\to \mathbb{R}^{3}$ . Обозначим локальные координаты на $\Gamma$ (т.е. координаты на ) через .

Пусть, далее, -- непрерывная вещественнозначная функция, определенная на $\Gamma$ .

Интеграл

$\displaystyle \iint\limits_{\Gamma}f dS\overset{\text{Опр.}}= \iint\limits_{D} f (\theta (u,v))\sqrt{\det (\theta'^{T}\theta')} dudv ,$

не зависит от выбора параметризации поверхности и называется поверхностным интегралом 1 рода. Здесь $\theta'^{T}$ -- матрица, транспонированная к матрице Якоби $\theta'$ . В координатном виде

$\displaystyle \det(\theta'^{T}\theta')=\left( \frac{D (y,z)}{D (u,v)} \right)^{... ...)}{D (u,v)} \right)^{2}+ \left( \frac{D (x,y)}{D (u,v)} \right)^{2}=EG-F^{2} ,$

где

$\displaystyle E$	$\displaystyle =\left\vert \frac{\partial\theta}{\partial u} \right\vert^{2}= \l... ... y}{\partial u} \right)^{2}+ \left(\frac{\partial z}{\partial u} \right)^{2} ,$
$\displaystyle F$	$\displaystyle = \frac{\partial\theta}{\partial u} \cdot \frac{\partial\theta}{\... ...\partial v}+ \frac{\partial z}{\partial u}\cdot\frac{\partial z}{\partial v} ,$
$\displaystyle G$	$\displaystyle =\left\vert \frac{\partial\theta}{\partial v} \right\vert^{2}= \l... ... y}{\partial v} \right)^{2}+ \left(\frac{\partial z}{\partial v} \right)^{2} .$

В случае явного задания поверхности

$\displaystyle \iint\limits_{\Gamma}f dS = \iint\limits_{D} f (x ,y,g (u,v)) \s... ...rtial x} \right)^{2}+ \left(\frac{\partial g}{\partial y} \right)^{2}} dxdy .$

Физический смысл поверхностного интеграла 1 рода 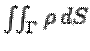$\iint_{\Gamma}\rho dS$ -- масса тонкой поверхности $\Gamma$ с поверхностной плотностью $\rho$ .

Ответ:8

Пусть $\Gamma$ -- ориентированная гладкая кривая с параметризацией $\gamma (t)\,,t\in[a,b]$ и пусть $\tau$ -- соответствующий единичный касательный вектор к $\Gamma$ . Пусть, далее, $\mathbf{F}$ -- векторное поле, определенное на $\Gamma$ . Криволинейный интеграл 1 рода вида

$\displaystyle \int\limits_{\Gamma} \mathbf{F}\cdot\tau\,dl$

называется криволинейным интегралом 2 рода по кривой $\Gamma$ . Этот интеграл меняет знак при изменении ориентации кривой.

В координатном виде

$\displaystyle \int\limits_{\Gamma} \mathbf{F}\cdot\tau\,dl= \int\limits_{a}^{b} (P (\gamma (t)) x' (t) +Q (\gamma (t)) y' (t))\,dt\,,$

где $\mathbf{F}= (P,Q)$ и $\gamma (t)= (x (t),y (t))$ . Интеграл в правой части равенства принято обозначать через

$\displaystyle \int\limits_{\Gamma}P (x,y)\,dx+Q (x,y)\,dy$

и называть интегралом от дифференциальной формы $P\,dx+Q\,dy$ .

Физический смысл интеграла 2 рода 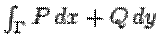$\int_{\Gamma}P\,dx+Q\,dy$ -- работа силы $\mathbf{F}= (P,Q)$ на пути $\Gamma$ .

Ответ: 9

Упомянутая запись выражается равенством

$\displaystyle \int\limits_{\Gamma}P (x,y) dx+Q (x,y) dy= \int\limits_{\Gamma} \mathbf{F}\cdot\tau dl$

где $\mathbf{F}= (P,Q)$ и $\tau$ -- единичный касательный вектор ориентированной кривой $\Gamma$ .

В координатном виде

$\displaystyle \int\limits_{\Gamma}P (x,y) dx+Q (x,y) dy= \int\limits_{\Gamma} [P (x,y)\cos\alpha+Q (x,y)\sin\alpha] dl ,$

где $\alpha$ -- угол между осью абсцисс и вектором $\tau$ .

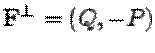Заметим, далее, что вектор $\mathbf{n}= (\sin\alpha,-\cos\alpha)$ является вектором нормали к кривой $\Gamma$ . Введем векторное поле $\mathbf{F}^{\perp}= (Q,-P)$ . Тогда

$\displaystyle \int\limits_{\Gamma}P\,dx+Q\,dy= \int\limits_{\Gamma} \mathbf{F}^{\perp}\cdot \mathbf{n}\,dl\,.$

Это еще одна запись криволинейного интеграла 2 рода через интеграл 1 рода.

Ответ:15

Ориентация связной области на плоскости индуцируется ориентацией плоскости. Под ориентацией плоскости понимается один из двух классов эквивалентных между собой базисов, при этом два базиса считаются эквивалентными, если определитель матрицы перехода от одного базиса к другому положителен. Таким образом, ориентация определяется выбором базиса на плоскости.