Математика \ Математический анализ

Ответы на контрольные задания по теме: "Дифуры", страница 2

$\displaystyle (D - k_1)^{r_1}y=0$   и$\displaystyle \qquad(D - k_2)^{r_2}y = 0\,.$

Таким образом, общее решение рассматриваемого уравнения запишется как

$\displaystyle y(x)=P_{r_1-1}(x)e^{k_1x}+P_{r_2-1}(x)e^{k_2 x}\,,$

где функции $ P_{r_1-1}(x),P_{r_2-1}(x)$имеют вид многочленов степеней, соответственно, $ (r_1-1)$и $ (r_2-1)$с произвольными коэффициентами:

$\displaystyle P_{r_{1}-1} (x)=C_{1}x^{r_{1}-1}+\ldots+ C_{r_{1}}\,, \qquad P_{r_{2}-1} (x)=C_{r_{1}+1}x^{r_{2}-1}+\ldots+ C_{r_{1}+r_{2}}\,.$


Ответ:9

Рассматривается линейное неоднородное дифференциальное уравнение $ n$-го порядка с постоянными (вещественными) коэффициентами

$\displaystyle P_{n} (D)y=f (x) .$

Если правая часть в этом уравнении имеет вид произведения многочлена на экспоненту (возможно, с комплексным показателем) 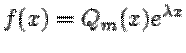$ f (x)=Q_{m} (x)e^{\lambda x}$, то частное решение рассматриваемого уравнения можно искать методом неопределенных коэффициентов. Именно, если число $ \lambda$является корнем кратности $ k$характеристического уравнения $ P_{n} (z)=0$(кратность 0 соответствует случаю, когда $ P_{n} (\lambda)\ne0$), то частное решение дифференциального уравнения можно искать в виде

$\displaystyle y=x^{k}S_{m} (x)e^{\lambda x}$

где $ S_{m}$-- многочлен степени $ m$, коэффициенты в котором подлежат определению.

Если правая часть имеет вид $ f (x)=Q_{m} (x) e^{\alpha x}\cos(\beta x)+ R_{l} (x)e^{\alpha x}\sin (\beta x)$, то в согласии с принципом суперпозиции решение можно искать в виде

$\displaystyle y=x^{k}e^{\alpha x} [U (x)\cos (\beta x)+V (x)\sin (\beta x)] \,,$

где $ k$-- кратность корней $ (\alpha\pm i\beta)$для символа $ P_{n} (z)$, а $ U,V$-- многочлены с неопределенными коэффициентами степени $ \max\{m,l\}$.

Ответ:10

Система двух линейных дифференциальных уравнений первого порядка имеет вид

\begin{displaymath}\begin{cases}y_{1}'=a_{11} (x)y_{1}+a_{12} (x)y_{2}+f_{1} (x)... ...y_{2}'=a_{21} (x)y_{1}+a_{22} (x)y_{2}+f_{2} (x) , \end{cases}\end{displaymath}

или, в матричной форме, 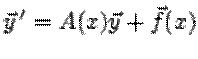$ \vec y '=A (x)\vec y+\vec f (x)$. Если 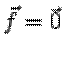$ \vec f=\vec0$, система называется однородной.

Множество решений однородной системы является двумерным векторным пространством, так что общее ее решение имеет вид

$\displaystyle \vec y= C_{1}\vec y_{1}+C_{2}\vec y_{2} ,$

где $ \vec y_{1}, \vec y_{2}$-- базис в пространстве решений (фундаментальная система решений).

Общее решение неоднородного уравнения имеет вид суммы частного его решения и общего решения однородного уравнения:

$\displaystyle \vec y=\vec y_{*}+C_{1}\vec y_{1}+C_{2}\vec y_{2}\,.$

Линейное уравнение 2-го порядка

$\displaystyle y''+p_{1} (x)y'+p_{0} (x)y=q (x)$

всегда можно свести к системе:

\begin{displaymath}\begin{cases}y_{1}'=y_{2} , y_{2}'=-p_{0} (x)y_{1}-p_{1} (x)y_{2}+q (x) . \end{cases}\end{displaymath}


Система уравнений не всегда может быть сведена к скалярному уравнению. Но, например, если коэффициенты $ a_{11},a_{12}$дифференцируемы и $ a_{12}\ne0$, то из первого уравнения можно выразить $ y_{2}$и подставить его во второе уравнение, получая скалярное линейное дифференциальное уравнение 2-го порядка для $ y_{1}$.

Ответ:11

Рассмотрим однородную систему линейных дифференциальных уравнений первого порядка

$\displaystyle \vec y\,'=A (x)\vec y\,.$

Пусть $ \vec y_{1},\ldots \vec y_{n}$-- некоторые ее решения. Определитель, составленный из этих решений как из столбцов, называется определителем Вронского системы

$\displaystyle W[\vec y_{1},\ldots \vec y_{n}] (x)= \vec y_{1}\wedge\ldots \wedge\vec y_{n}\,.$

Если решения $ \vec y_{1},\ldots \vec y_{n}$линейно зависимы, их определитель Вронского тождественно равен нулю. Обратно, если определитель Вронского решений равен нулю хотя бы в одной точке, то он равен нулю тождественно, а решения -- линейно зависимы.

Имеет силу, также, формула Лиувилля

$\displaystyle W (x)=W (x_{0})e^{\int\limits_{x_{0}}^{x} \mathrm{tr\,}A (t)\,dt}\,.$

Ответ: 12

Уравнения механических и электрических колебаний это линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. Например, если материальная точка массы $ m$совершает вынужденные колебания под действием силы $ f (t)$в системе с коэффициентом Гука $ k$и коэффициентом трения $ \gamma$, то по второму закону Ньютона

$\displaystyle mx''=f (t)-kx-\gamma x'\,.$

В случае простого электрического колебательного контура падение напряжения на сопротивлении, емкости и индуктивности равно соответственно $ RI, q/C,LI'$, где $ R$-- сопротивление, $ I$-- ток, $ q$-- заряд, $ C$-- емкость и $ L$-- индуктивность. Тогда колебания тока в цепи подчиняются уравнению

$\displaystyle RI'+ \frac{I}{C}+LI''= \mathcal{E}' ,$

где $ \mathcal{E}$-- напряжение на источнике питания.

Ответ: 13

Рассмотрим, вначале, вынужденные колебания вида

$\displaystyle x''+\omega^{2}x=A\sin(\nu t)\,.$


Собственные колебания системы имеют частоту $ \omega$и вид

$\displaystyle x=C_{1}\cos (\omega t)+ C_{2}\sin (\omega t)\,.$

Если $ \nu\ne\omega$, то вынужденные колебания будут проходить с частотой $ \nu$и иметь вид

$\displaystyle x=B_{1}\cos (\nu t)+B_{2}\sin (\nu t)\,.$

Если же $ \nu=\omega$, то вынужденные колебания будут уже иметь вид

$\displaystyle x=t[B_{1}\cos (\omega t)+B_{2}\sin (\omega t)]\,.$


Это явление -- неограниченный рост амплитуды вынужденных колебаний при совпадении частоты вынужденных колебаний с частотой собственных колебаний -- носит название резонанса.

Более общо, если в уравнении

$\displaystyle P_{n} (D)y=Q_{m} (x)e^{\alpha x}\cos (\beta x)+ R_{l} (x)e^{\alpha x}\sin (\beta x)$

характеристические числа правой части $ \alpha\pm i\beta$являются корнями символа оператора левой части (корнями характеристического уравнения), то также говорят о резонансе. Он проявляется в том, что частное решение такого уравнения приходится искать в виде

$\displaystyle y=x^{k}e^{\alpha x}[U (x)\cos (\beta x)+ V (x)\sin (\beta x)]\,,$

где $ U,V$-- многочлены максимальной степени из $ m,l$, а $ k$-- кратность корней $ (\alpha\pm i\beta)$. Т.е. в результате резонанса решение получает дополнительный степенной множитель

Ответ: 14

Разрешающий оператор $ R (x,x_{0})$системы дифференциальных уравнений

$\displaystyle \vec y\,'=A (x)\vec y$


является матричным решением задачи Коши

$\displaystyle Y'=A (x)Y\,,\qquad Y (x_{0})=I\,.$

Рассмотрим систему двух уравнений и пусть $ \vec y_{1}, \vec y_{2}$-- два ее линейно независимых решения (фундаментальная система решений). Для произвольной точки $ x_{0}$найдем решения $ A_{1},A_{2},B_{1},B_{2}$алгебраических уравнений

Скачать файл