Основные понятия физики плазмы. Электродинамика быстрых процессов в плазме, страница 8

            Если источник локализован на оси  плазменного цилиндра радиуса , то

везде, кроме  будем иметь уравнение

                                                .

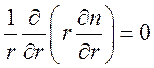Граничное условие возьмем в виде .Получаем представление

                                                .

Благодаря чрезмерной идеализации постановки задачи (источник бесконечно тонкий) имеется обращение концентрации в бесконечность.

13.8. Влияние внешнего магнитного поля, анизотропия плазмы. Исследуем влияние постоянного, однородного внешнего магнитного поля  на распространение плоских монохроматических волн малой амплитуды (линейное приближение) в холодной (), бесстолкновительной плазме (), считая ионы неподвижными (высокочастотное приближение). Ниже будет показано, что наличие внешнего магнитного поля делает плазму анизотропной средой.

Система уравнений Максвелла

                                               

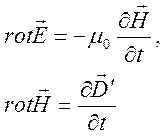
в случае линейных волн, распространяющихся в однородной среде, сводится к векторному алгебраическому уравнению для фурье – образа

                                                                              (13.2)

Член  можно представить в виде 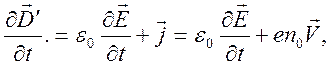 и для фурье – образов получим связь 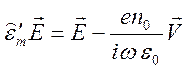. Это позволяет (13.2) представить в виде

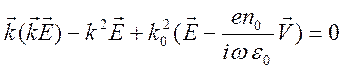                        .                                      (13.3)

Для того, чтобы получить дисперсионное уравнение, описывающее электродинамические свойства плазмы, необходимо установить связь между  и . Ограничимся исследованием двух частных случаев: 1). Поперечное распространение волн  и 2). Продольное распространение волн 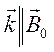. Декартову систему координат ориентируем так, что .

            1). Поперечное распространение волн ,  (Рис.13.3). Представим электрическое поле в виде суммы продольной и поперечной компонент . Магнитное поле не оказывает влияния на движение электронов в случае  и , поэтому такая волна называется обыкновенной. В этом случае получается известный результат (выпишем его с учетом соударений)

                                    .

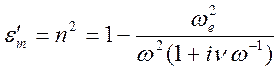В случае  волна называется необыкновенной.

Уравнение движения для фурье – образов полей имеет вид (индекс  у вектора скорости электронов опустим)

                                                .

Проекции этого уравнения на оси  и :

                                                ,

                                                .

Отсюда получаем представления

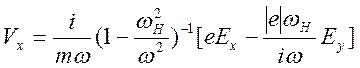                                    ,                       (13.4)

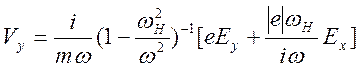                                    .                       (13.5)

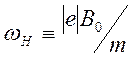 - циклотронная частота электронов (частота гирорезонанса электронов).

Условие разрешимости алгебраической системы (13.3)-(13.5) дает дисперсионное уравнение для описания необыкновенной волны.

                                    ,

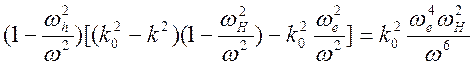где  - верхнегибридная частота. Решение дисперсионного уравнения для волны необыкновенной можно представит в виде

                                                .

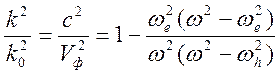            2. Продольное распространение волн 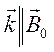 (Рис.13.4). В этом случае поле  также лежит в плоскости, перпендикулярной волновому вектору . Соотношения (13.4) и (13.5) остаются применимыми в этой ситуации. Так как , то уравнение (13.2)принимает вид

                                    ,

                                    .

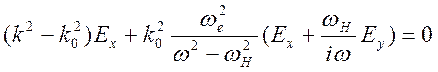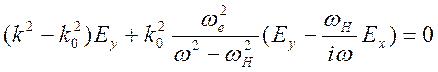Дисперсионное уравнение дает решение в виде

                                    .

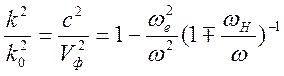Знакиотносятся к волнам правой  и левой поляризации. Вектор  в волне правой поляризации вращается по часовой стрелке, если смотреть по направлению вектора . В волне левой поляризации вращение происходит в противоположную сторону. Эти две волны распространяются с различными скоростями. Это приводит к фарадееву вращению плоскости поляризации.

            В случае произвольного угла между векторами  и  свойства плазмы становятся еще более сложными, чем в рассмотренных двух предельных случаях.

13.9. Диффузия слабоионизированной плазмы поперек магнитного поля.