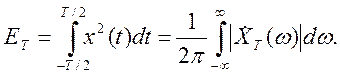
Разделив эту энергию на Т, получим среднюю мощность РТ реализации на данном временном интервале:
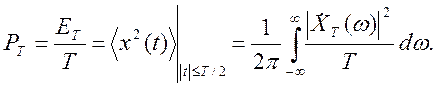 (4.1)
(4.1)
При увеличении длительности промежутка времени Т
энергия отрезка реализации неограниченно возрастает, а средняя мощность стремится
к некоторому пределу. Совершив предельный переход Т ®¥,
получим: 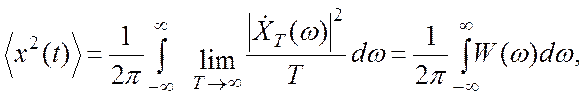
где функция
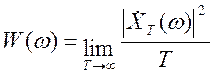 (4.2
(4.2
представляет собой спектральную плотность средней мощности рассматриваемой реализации.
Замечание. Для краткости часто говорят "спектральная плотность мощности" или "спектр мощности".
В общем случае спектральную плотность мощности W(ω) необходимо усреднить по множеству реализаций ансамбля. Однако, если ограничиться рассмотрением эргодических процессов, можно считать, что найденная по одной реализации (путем усреднения по времени) функция W(ω) характеризует весь процесс в целом.
Энергетический спектр случайного процесса можно определить в рамках корреляционного анализа. Найдем связь энергетического спектра и корреляционной функции.
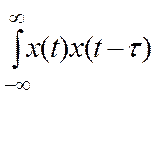 Согласно (3.3) для центрированного процесса корреляционная
функция в бесконечных пределах равна:
Согласно (3.3) для центрированного процесса корреляционная
функция в бесконечных пределах равна:
R(t) = d t
Второй сомножитель под интегралом выразим через обратное преобразование Фурье.
Tогда:
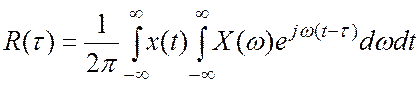
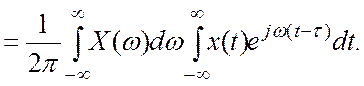 (4.3)
(4.3)
Второй интеграл в (4.3) дает комплексно – сопряженное
значение спектральной плотности ![]() .
Отсюда
.
Отсюда
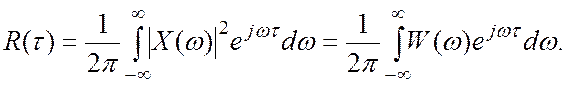 (4.4)
(4.4)
Следовательно, корреляционная функция есть обратное преобразование Фурье от энергетического спектра.
Раз существует обратное преобразование Фурье, можно записать и прямое преобразование:
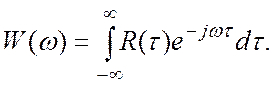 (4.5)
(4.5)
Таким образом, корреляционная функция случайного процесса и его спектральная плотность связаны друг с другом преобразованием Фурье. Это соотношение носит название теоремы Винера - Хинчина.
Функция взаимной корреляции. Выше отмечалось, что корреляционная функция случайного процесса есть мера статистической связи между двумя значениями процесса, разделёнными промежутком t. Если имеются два случайных процесса – x(t) и y(t) можно оценить наличие статистической связи между ними вычислив функцию взаимной корреляции:
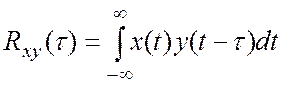 (4.6)
(4.6)
Заметим, что функция взаимной
корреляции функция не обладает свойствами обычной корреляционной функции одиночного
процесса. В частности, её максимум может не совпадать со значением t = 0. Кроме того, она не является
обязательно чётной. В этой связи, чтобы избежать недоразумений, функцию R(t) одиночного
процесса часто называют автокорреляционной функцией. Функция (4,6)
называется взаимокорреляционной. Пользуясь теоремой Винера – Хинчина,
можно определить так называемый взаимный энергетический спектр процессов
![]() и
и ![]() .
.
Эффективная ширина спектра. Пусть исследуемый случайный процесс характеризуется спектром плотности мощности W(ω), имеющим максимальное значение Wтах. Заменим мысленно данный случайный процесс другим, у которого спектральная плотность мощности постоянна и равна Wтах пределах некоторой полосы частот, выбираемой из условия равенства средних мощностей обоих процессов. Ширина этой полосы частот называется эффективной шириной спектра случайного процесса:
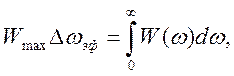
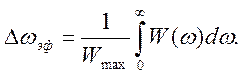
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.