Осесимметрические задачи теории упругости. Состояние упругости. Закон Гука. Решение системы линейных уравнений с ленточной матрицей коэффициентов

Аннотация

1. Осесимметрические задачи теории упругости………………………….стр. 2

2.   Состояние упругости. Закон Гука………………………………………..стр. 6

     3.   Решение системы линейных уравнений с

            ленточной матрицей  коэффициентов……………………………..……стр. 9

     4.   Подпрограмма GELB……………………………………………..………стр. 9

      5.   Подпрограмма DGELB…………………………………………………...стр. 12

      6.   Список использованной литературы……………………………………стр. 15

                           Осесимметрические задачи теории упругости

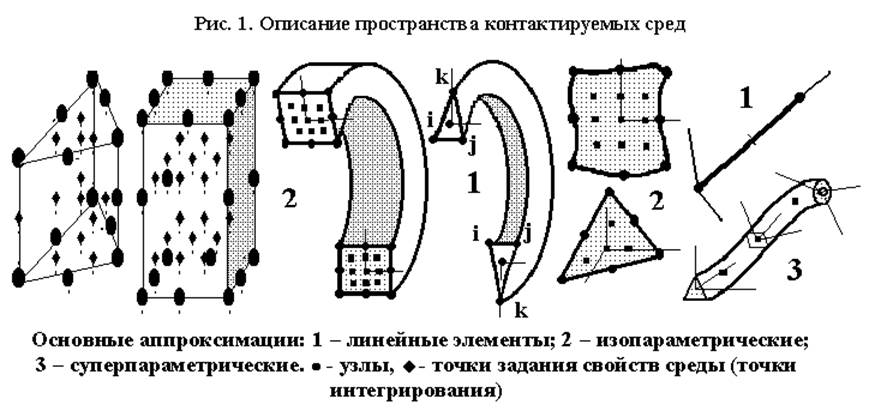
Важный класс задач теории упругости включает задачи, в которых рассматрива-ются тела вращения при осесимметричном нагружении. Хотя такие тела и явля-ются трехмерными, но ни их геометрия, ни условия нагружения не зависят от ази-мутальной координаты. Поэтому при решении может быть использован тот же подход, что и к двумерным задачам. Осесимметричный треугольный элемент, по-лученный вращением треугольного симплекс-элемента, образует треугольный тор (см. рис.1, аппроксимация 1).

Нанести на рисунок оси rzq

   Необходимо записать несколько соотношений, потому что удобнее использовать компоненты тензоров напряжения и деформаций в цилиндрической системе координат. Здесь представлены основные величины: компоненты вектора напряжений

компоненты вектора деформаций

Соотношения связи между деформациями и перемещениями имеют вид

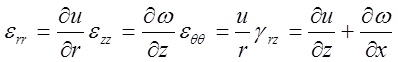
Предполагая материал изотропным, запишем матрицу упругих характеристик

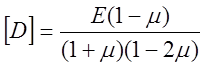
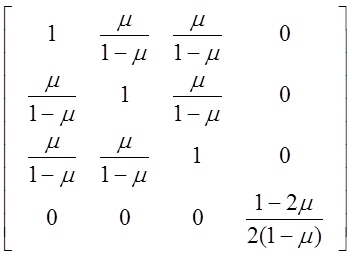
и вектор начальной деформации, вызванной тепловым воздействием,

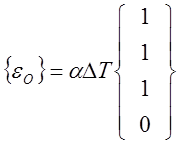
  Поле перемещений внутри элемента аппроксимируются соотношениями, где     функции формы выражаются через r и z, а перемещения обозначаются буквами u и w.

ЭТО ИЗОБРАЖЕНИЕ ПРЕОБРАЗОВАТЬ  в РИСУНОК !  ***.bmp

     Z 

                 

                                                                          s_xz

                                                                                                       t_zr

                                                                 s_rr

                                                              t_rz                         s_qq

                          q

                        r

   рис.1.Компоненты напряжений в осесимметрических задачах.

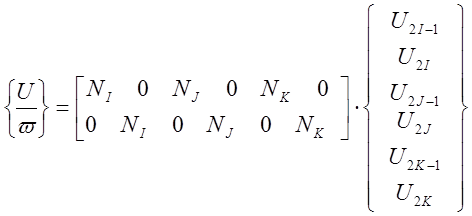
Дифференцируя это выражение и используя соотношение связи между деформациями и перемещениями ,получаем

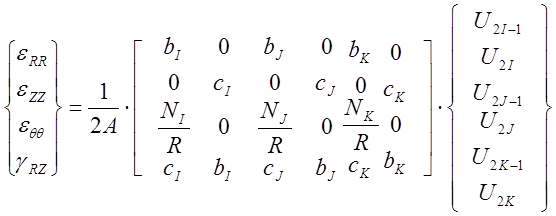
Матрица коэффициентов соответствует, так как  .

Вычисление интегралов, определяющих матрицы элементов, несколько сложнее, чем это было в одномерных, двумерных и трехмерных задачах. Матрица             содержит теперь коэффициенты, являющиеся функциями координат, и не может быть вынесена за знак интеграла.

Матрицу жесткости можно определить, вычислив   по значениям R  и Z  в центре элемента. Такой способ позволяет выносить матрицу     из-под интеграла:

                                                 

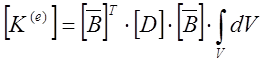
Учитывая, что объём элемента дается формулой

V=2

 где A-площадь поперечного сечения элемента, получаем для     окончательное выражение:

                                              

Черта над    указывает на приближенное значение. Формула приближенная, но она дает приемлемые результаты, если разбиение на элементы согласуется с ожидаемым распределением  напряжений ,т.е. в области с большими значениями

градиентов напряжений используются малые элементы и т.д.

Вектор-столбец, связанный с тепловым расширением, определяется точно так же ,поскольку под интегралом стоит матрица . Приближенное соотношение получается вычислением  по значениям  и    для данного элемента. Приведем окончательный результат:

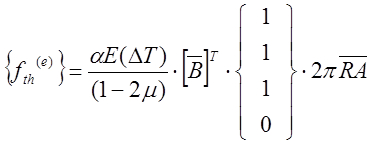
Объемный интеграл от объемных сил может быть проинтегрирован точно с использованием L-координат или приближенного метода. Этот интеграл выражается через L-координаты следующим образом:

                                     

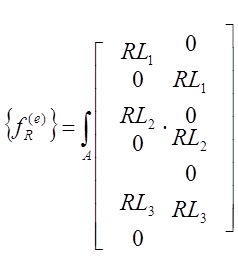
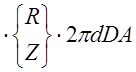
где dV   заменено на     радиальное расстояние r также может быть выражено через L-координаты:

         (*)

подстановка этого выражения в предыдущее приводит к произведению типа        или   . Окончательно получаем

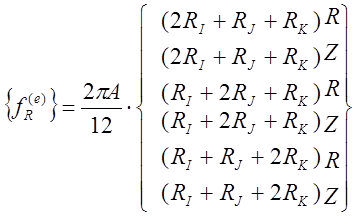
Соотношение показывает, что компоненты объемной силы R  или Z  не распределяются в данном случае поровну между тремя узлами элемента. Большая часть приходится на узлы, наиболее удаленные от оси вращения.